Question

Let $\alpha$, $\beta$, $\gamma$ be distinct real numbers such that $a\alpha^2 + b\alpha + c = (sin\theta)\alpha^2 + (cos\theta)\alpha$ $a\beta^2 + b\beta + c = (sin\theta)\beta^2 + (cos\theta)\beta$ $a\gamma^2 + b\gamma + c = (sin\theta)\gamma^2 + (cos\theta)\gamma$ (where a, b, c $\in$ R)

Find the maximum value of the expression $\frac{a^2 + b^2}{a^2 + 3ab + 5b^2}$

Answer 1

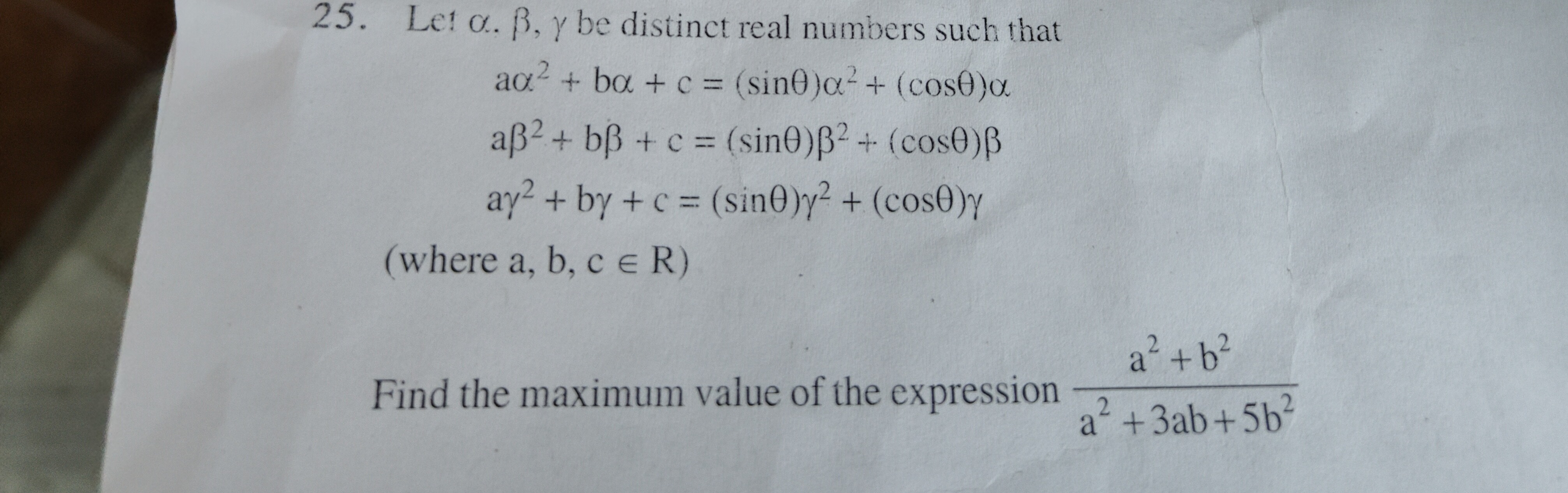
2

Answer 2

The given equations are:

1. $a\alpha^2 + b\alpha + c = (\sin\theta)\alpha^2 + (\cos\theta)\alpha$
2. $a\beta^2 + b\beta + c = (\sin\theta)\beta^2 + (\cos\theta)\beta$
3. $a\gamma^2 + b\gamma + c = (\sin\theta)\gamma^2 + (\cos\theta)\gamma$

Rearranging these equations, we get:

1. $(a - \sin\theta)\alpha^2 + (b - \cos\theta)\alpha + c = 0$
2. $(a - \sin\theta)\beta^2 + (b - \cos\theta)\beta + c = 0$
3. $(a - \sin\theta)\gamma^2 + (b - \cos\theta)\gamma + c = 0$

Let $P(x) = (a - \sin\theta)x^2 + (b - \cos\theta)x + c$.

We are given that $\alpha$, $\beta$, $\gamma$ are distinct real numbers and they are roots of the quadratic polynomial $P(x) = 0$.

A non-zero quadratic polynomial can have at most two distinct real roots. Since $P(x)$ has three distinct real roots, it must be the zero polynomial.

This implies that all its coefficients must be zero:

$a - \sin\theta = 0 \implies a = \sin\theta$

$b - \cos\theta = 0 \implies b = \cos\theta$

$c = 0$

Now we need to find the maximum value of the expression $\frac{a^2 + b^2}{a^2 + 3ab + 5b^2}$.

Substitute $a = \sin\theta$ and $b = \cos\theta$ into the expression:

Expression $E = \frac{(\sin\theta)^2 + (\cos\theta)^2}{(\sin\theta)^2 + 3(\sin\theta)(\cos\theta) + 5(\cos\theta)^2}$

We know that $\sin^2\theta + \cos^2\theta = 1$.

So, $E = \frac{1}{\sin^2\theta + 3\sin\theta\cos\theta + 5\cos^2\theta}$

To find the maximum value of $E$, we need to find the minimum value of the denominator.

Let $D = \sin^2\theta + 3\sin\theta\cos\theta + 5\cos^2\theta$.

We can rewrite $D$ using double angle formulas:

$\sin^2\theta = \frac{1 - \cos(2\theta)}{2}$

$\cos^2\theta = \frac{1 + \cos(2\theta)}{2}$

$2\sin\theta\cos\theta = \sin(2\theta)$

Substitute these into $D$:

$D = \frac{1 - \cos(2\theta)}{2} + \frac{3}{2}\sin(2\theta) + 5\left(\frac{1 + \cos(2\theta)}{2}\right)$

$D = \frac{1}{2} - \frac{1}{2}\cos(2\theta) + \frac{3}{2}\sin(2\theta) + \frac{5}{2} + \frac{5}{2}\cos(2\theta)$

$D = \left(\frac{1}{2} + \frac{5}{2}\right) + \left(-\frac{1}{2} + \frac{5}{2}\right)\cos(2\theta) + \frac{3}{2}\sin(2\theta)$

$D = 3 + 2\cos(2\theta) + \frac{3}{2}\sin(2\theta)$

To find the minimum value of $D$, we need to find the minimum value of the trigonometric expression $2\cos(2\theta) + \frac{3}{2}\sin(2\theta)$.

For an expression of the form $A\cos x + B\sin x$, its minimum value is $-\sqrt{A^2+B^2}$.

Here, $A = 2$ and $B = \frac{3}{2}$.

So, the minimum value of $2\cos(2\theta) + \frac{3}{2}\sin(2\theta)$ is $-\sqrt{2^2 + \left(\frac{3}{2}\right)^2}$:

$-\sqrt{4 + \frac{9}{4}} = -\sqrt{\frac{16+9}{4}} = -\sqrt{\frac{25}{4}} = -\frac{5}{2}$.

Therefore, the minimum value of $D$ is $3 - \frac{5}{2} = \frac{6-5}{2} = \frac{1}{2}$.

The maximum value of the expression $E$ occurs when the denominator $D$ is at its minimum value:

Maximum $E = \frac{1}{\text{minimum } D} = \frac{1}{1/2} = 2$.