Question

If $A = \begin{bmatrix} 1 & 3 & 3 \\ 1 & 4 & 4 \\ 1 & 3 & 4 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 12 \\ 15 \\ 13 \end{bmatrix}$ then the values of x, y, z respectively are

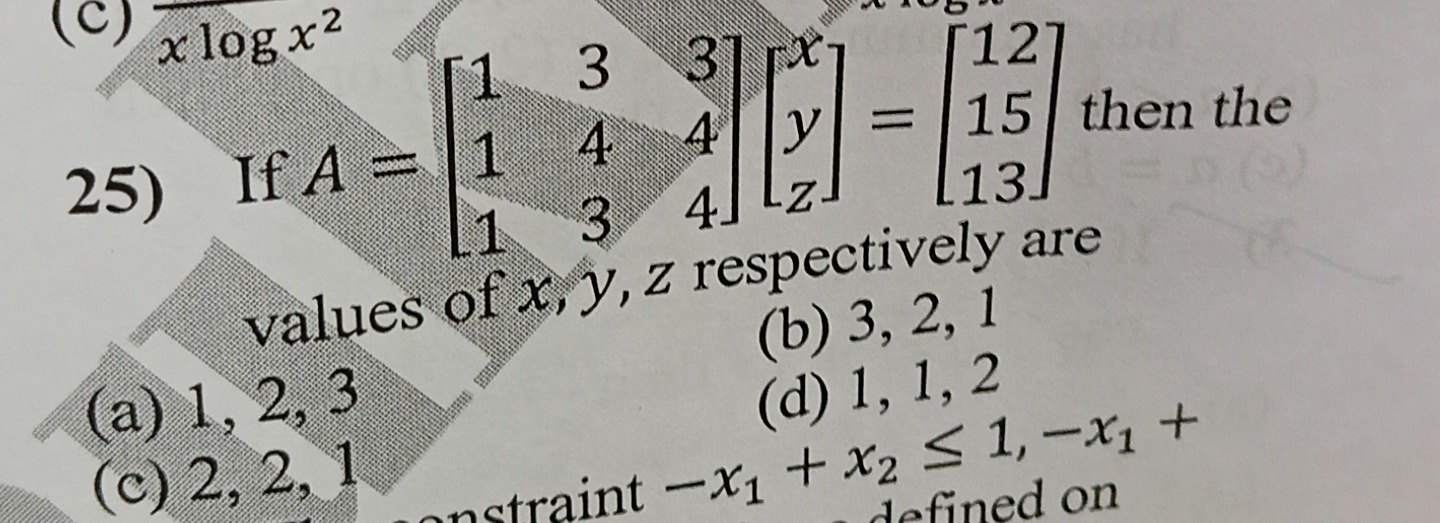
• A. 1, 2, 3
• B. 3, 2, 1
• C. 2, 2, 1
• D. 1, 1, 2

Answer 1

Answer: (B)

3, 2, 1

Answer 2

Given the system:

$$\begin{aligned} x + 3y + 3z &= 12 \quad \text{(1)}\\[5mm] x + 4y + 4z &= 15 \quad \text{(2)}\\[5mm] x + 3y + 4z &= 13 \quad \text{(3)} \end{aligned}$$

Subtract (1) from (2):

$$(x + 4y + 4z) - (x + 3y + 3z) = 15 - 12 \quad \Rightarrow \quad y + z = 3 \quad \text{(4)}$$

Subtract (1) from (3):

$$(x + 3y + 4z) - (x + 3y + 3z) = 13 - 12 \quad \Rightarrow \quad z = 1$$

Substitute $z = 1$ in (4):

$$y + 1 = 3 \quad \Rightarrow \quad y = 2$$

Now substitute $y = 2$ and $z = 1$ in (1):

$$x + 3(2) + 3(1) = 12 \quad \Rightarrow \quad x + 6 + 3 = 12 \quad \Rightarrow \quad x = 12 - 9 = 3$$

Thus, $x = 3$, $y = 2$, $z = 1$.