Question
Question: Four point charges A, B, C and D are placed at the four corners of a square of side a. The energy re...
Four point charges A, B, C and D are placed at the four corners of a square of side a. The energy required to take the charges C and D to infinity (they are also infinitely separated from each other) is
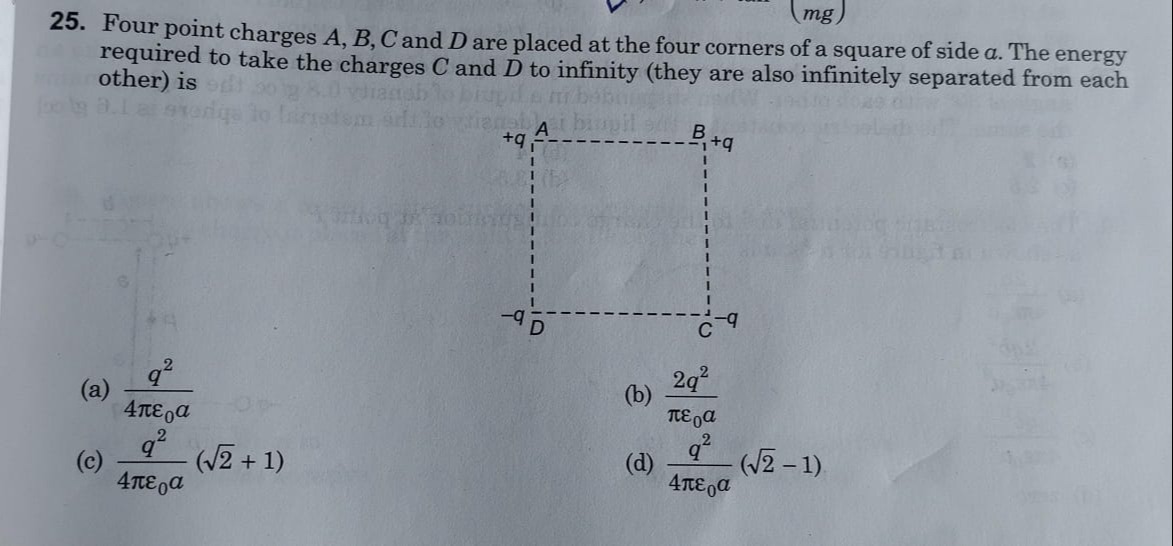
4πϵ0aq2
πϵ0a2q2
4πϵ0aq2(2+1)
4πϵ0aq2(2−1)
4πϵ0aq2(2+1)
Solution
The initial potential energy of the system of four charges is the sum of the potential energies of all pairs of charges: Uinitial=∑i<j4πϵ0rijqiqj
The charges are qA=+q, qB=+q, qC=−q, qD=−q. The side length of the square is a.
The distances between the charges are: rAB=rBC=rCD=rDA=a (adjacent sides) rAC=rBD=a2 (diagonals)
Uinitial=4πϵ01(rABqAqB+rACqAqC+rADqAqD+rBCqBqC+rBDqBqD+rCDqCqD)
Substituting the charges and distances: Uinitial=4πϵ01(a(+q)(+q)+a2(+q)(−q)+a(+q)(−q)+a(+q)(−q)+a2(+q)(−q)+a(−q)(−q)) Uinitial=4πϵ01(aq2−a2q2−aq2−aq2−a2q2+aq2) Uinitial=4πϵ0aq2(1−21−1−1−21+1) Uinitial=4πϵ0aq2((1−1−1+1)−(21+21)) Uinitial=4πϵ0aq2(0−22)=4πϵ0aq2(−2)=−4πϵ0a2q2
The final state is when charges C and D are at infinity. Charges A and B remain at their original positions. The potential energy of the system in the final state is the potential energy of the remaining charges A and B. Ufinal=4πϵ0rABqAqB=4πϵ0a(+q)(+q)=4πϵ0aq2
The energy required to take charges C and D to infinity is the work done by an external agent, which is equal to the change in potential energy of the system: Wext=Ufinal−Uinitial Wext=4πϵ0aq2−(−4πϵ0a2q2) Wext=4πϵ0aq2+4πϵ0a2q2 Wext=4πϵ0aq2(1+2)
