Question
Question: Determine the range of values of $\theta \in[0,2 \pi]$ for which the point $(\cos \theta, \sin \thet...
Determine the range of values of θ∈[0,2π] for which the point (cosθ,sinθ) lies inside the triangle formed by the lines x+y=2;x−y=1 & 6x+2y−10=0.
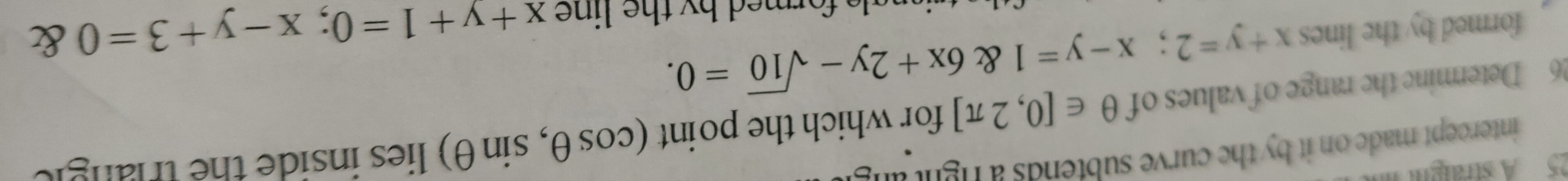
(0,arctan(31)+3π)
Solution
The problem asks for the range of values of θ∈[0,2π] for which the point P(cosθ,sinθ) lies inside the triangle formed by the lines:
L1:x+y−2=0 L2:x−y−1=0 L3:6x+2y−10=0
For a point to lie inside a triangle, it must satisfy certain conditions with respect to each line. The standard method is to check the sign of the expression Ax+By+C for the point with respect to each line, ensuring that it is the same as the sign for the third vertex (the vertex not lying on that line).
Let's find the vertices of the triangle:
-
Vertex A (L1∩L2): x+y=2 x−y=1 Adding the equations gives 2x=3⇒x=3/2. Subtracting the second from the first gives 2y=1⇒y=1/2. So, A=(3/2,1/2).
-
Vertex B (L1∩L3): x+y=2⇒y=2−x 6x+2y=10 Substitute y: 6x+2(2−x)=10⇒6x+4−2x=10⇒4x=10−4⇒x=(10−4)/4. y=2−(10−4)/4=(8−10+4)/4=(12−10)/4. So, B=((10−4)/4,(12−10)/4).
-
Vertex C (L2∩L3): x−y=1⇒y=x−1 6x+2y=10 Substitute y: 6x+2(x−1)=10⇒6x+2x−2=10⇒8x=10+2⇒x=(10+2)/8. y=(10+2)/8−1=(10−6)/8. So, C=((10+2)/8,(10−6)/8).
Now, we check the conditions for P(cosθ,sinθ) to be inside the triangle:
Condition 1: For L1:x+y−2=0. The third vertex is C=((10+2)/8,(10−6)/8). Evaluate L1(C)=(10+2)/8+(10−6)/8−2=(210−4)/8−2=(10−2)/4−2=(10−10)/4. Since 10≈3.16, L1(C)<0. So, for P(cosθ,sinθ) to be on the same side of L1 as C, we must have: cosθ+sinθ−2<0. The maximum value of cosθ+sinθ is 12+12=2. So, cosθ+sinθ−2≤2−2≈1.414−2=−0.586<0. This condition is always true for any point on the unit circle.
Condition 2: For L2:x−y−1=0. The third vertex is B=((10−4)/4,(12−10)/4). Evaluate L2(B)=(10−4)/4−(12−10)/4−1=(210−16)/4−1=(10−8)/2−1=(10−10)/2. Since 10≈3.16, L2(B)<0. So, for P(cosθ,sinθ) to be on the same side of L2 as B, we must have: cosθ−sinθ−1<0⇒cosθ−sinθ<1. We can write cosθ−sinθ=2cos(θ+π/4). So, 2cos(θ+π/4)<1⇒cos(θ+π/4)<1/2. Let α=θ+π/4. Since θ∈[0,2π], α∈[π/4,2π+π/4]=[π/4,9π/4]. For cosα<1/2 in the interval [π/4,9π/4], we have: π/4<α<7π/4. Substituting back α=θ+π/4: π/4<θ+π/4<7π/4 0<θ<3π/2.
Condition 3: For L3:6x+2y−10=0. The third vertex is A=(3/2,1/2). Evaluate L3(A)=6(3/2)+2(1/2)−10=9+1−10=10−10. Since 10≈3.16, L3(A)>0. So, for P(cosθ,sinθ) to be on the same side of L3 as A, we must have: 6cosθ+2sinθ−10>0⇒6cosθ+2sinθ>10. We can write 6cosθ+2sinθ=62+22cos(θ−ϕ)=36+4cos(θ−ϕ)=40cos(θ−ϕ)=210cos(θ−ϕ), where tanϕ=2/6=1/3. So, 210cos(θ−ϕ)>10⇒cos(θ−ϕ)>1/2. Let β=θ−ϕ. We need cosβ>1/2. We know ϕ=arctan(1/3). Since 0<1/3<1/3, we have 0<ϕ<π/6. So, ϕ≈0.322 radians (18.43∘). Since θ∈[0,2π], β=θ−ϕ∈[−ϕ,2π−ϕ]. For cosβ>1/2, we have β∈(−π/3,π/3) (modulo 2π). So, −π/3<θ−ϕ<π/3. ϕ−π/3<θ<ϕ+π/3. Numerically, π/3≈1.047 radians. So, 0.322−1.047<θ<0.322+1.047. −0.725<θ<1.369. Considering θ∈[0,2π], this interval becomes: 0≤θ<ϕ+π/3.
Combining the conditions:
- 0<θ<3π/2
- 0≤θ<ϕ+π/3
We need to find the intersection of these two ranges. The final range for θ is 0<θ<min(3π/2,ϕ+π/3). We know ϕ<π/6. So ϕ+π/3<π/6+π/3=π/2. Since π/2<3π/2, the intersection is 0<θ<ϕ+π/3.
The range of values for θ is (0,arctan(1/3)+π/3).
