Question
Question: A particle is projected with a speed u at an angle $\theta$ with the horizontal. Consider a small pa...
A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circle?
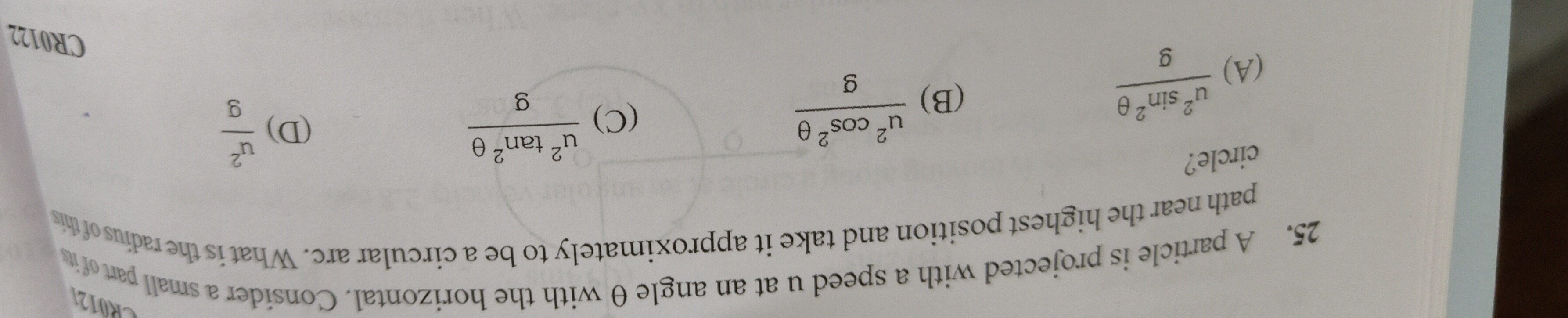
gu2sin2θ
gu2cos2θ
gu2
(B) gu2cos2θ
Solution
To find the radius of curvature of the projectile's path near its highest position, we consider the forces acting on the particle at that point and its velocity.
-
Velocity at the highest point:
When a particle is projected with an initial speed u at an angle θ with the horizontal, its velocity components are:- Horizontal component: vx=ucosθ
- Vertical component: vy=usinθ−gt
At the highest point of its trajectory, the vertical component of velocity (vy) becomes zero. The horizontal component of velocity (vx) remains constant throughout the motion (ignoring air resistance).
Therefore, the velocity of the particle at the highest point is v=ucosθ and it is directed horizontally. -
Force at the highest point:
At the highest point, the only force acting on the particle is gravity, which is directed vertically downwards. The magnitude of this force is F=mg. -
Radius of curvature:
For a particle moving along a curved path, the force component perpendicular to the velocity provides the centripetal force required for the circular motion (or the instantaneous circular arc).
At the highest point, the velocity is horizontal, and the gravitational force is vertical. Thus, the gravitational force is perpendicular to the velocity.
Therefore, the gravitational force provides the necessary centripetal force.The centripetal force is given by Fc=Rmv2, where m is the mass of the particle, v is its speed, and R is the radius of curvature.
Equating the gravitational force to the centripetal force at the highest point:
mg=Rmv2Substitute the velocity at the highest point, v=ucosθ:
mg=Rm(ucosθ)2Cancel m from both sides:
g=R(ucosθ)2Solve for R:
R=g(ucosθ)2
R=gu2cos2θ
The radius of the circular arc approximately representing the path near the highest position is gu2cos2θ.
Explanation of the solution: At the highest point of projectile motion, the velocity is purely horizontal, v=ucosθ. The only force acting is gravity, F=mg, directed vertically downwards. Since the force is perpendicular to the velocity, it provides the centripetal force. Equating mg=Rmv2 and substituting v=ucosθ, we get R=gu2cos2θ.
