Question
Question: The value of $\frac{\sum\limits_{r=1}^{n} \frac{1}{r}}{\sum\limits_{k=1}^{n}\frac{k}{(2n-2k+1)(2n-k+...
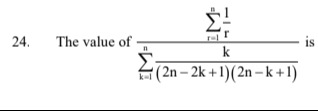
The value of k=1∑n(2n−2k+1)(2n−k+1)kr=1∑nr1 is
Answer
2
Explanation
Solution
Solution:
We are given
S=∑k=1n(2n−2k+1)(2n−k+1)k∑r=1nr1.Let
Hn=r=1∑nr1.Focus on the denominator:
D=k=1∑n(2n−2k+1)(2n−k+1)k.Step 1. Replace k by n−j, where j=0,1,2,…,n−1. Then:
2n−2k+1=2n−2(n−j)+1=2j+1, 2n−k+1=2n−(n−j)+1=n+j+1.Thus,
D=j=0∑n−1(2j+1)(n+j+1)n−j.Step 2. Write the general term in partial fractions:
(2j+1)(n+j+1)n−j=2j+1A+n+j+1B.Multiplying both sides by (2j+1)(n+j+1) gives:
n−j=A(n+j+1)+B(2j+1).Comparing coefficients:
- Coefficient of j: A+2B=−1.
- Constant term: A(n+1)+B=n.
Solving A+2B=−1 gives A=−1−2B. Substitute into the constant term:
(−1−2B)(n+1)+B=n⟹−(n+1)−2B(n+1)+B=n, −(n+1)−B(2n+2−1)=n, −(n+1)−(2n+1)B=n.Thus,
(2n+1)B=−(n+1+n)=−(2n+1)⟹B=−1.Then, A=−1−2(−1)=1.
So,
(2j+1)(n+j+1)n−j=2j+11−n+j+11.Step 3. Substitute back in the sum:
D=j=0∑n−1[2j+11−n+j+11]=S1j=0∑n−12j+11−S2j=0∑n−1n+j+11.Note that S2=∑m=n+12nm1=H2n−Hn.
Also, S1 is the sum of reciprocals of the first n odd numbers:
S1=11+31+⋯+2n−11=H2n−21Hn,since the sum of reciprocals for even numbers (up to 2n) is 21Hn.
Thus,
D=(H2n−2Hn)−(H2n−Hn)=Hn−2Hn=2Hn.Step 4. Now, the overall expression becomes:
S=2HnHn=2.