Question

The joint equation of the lines through the origin, trisecting angles in first and third quadrants is

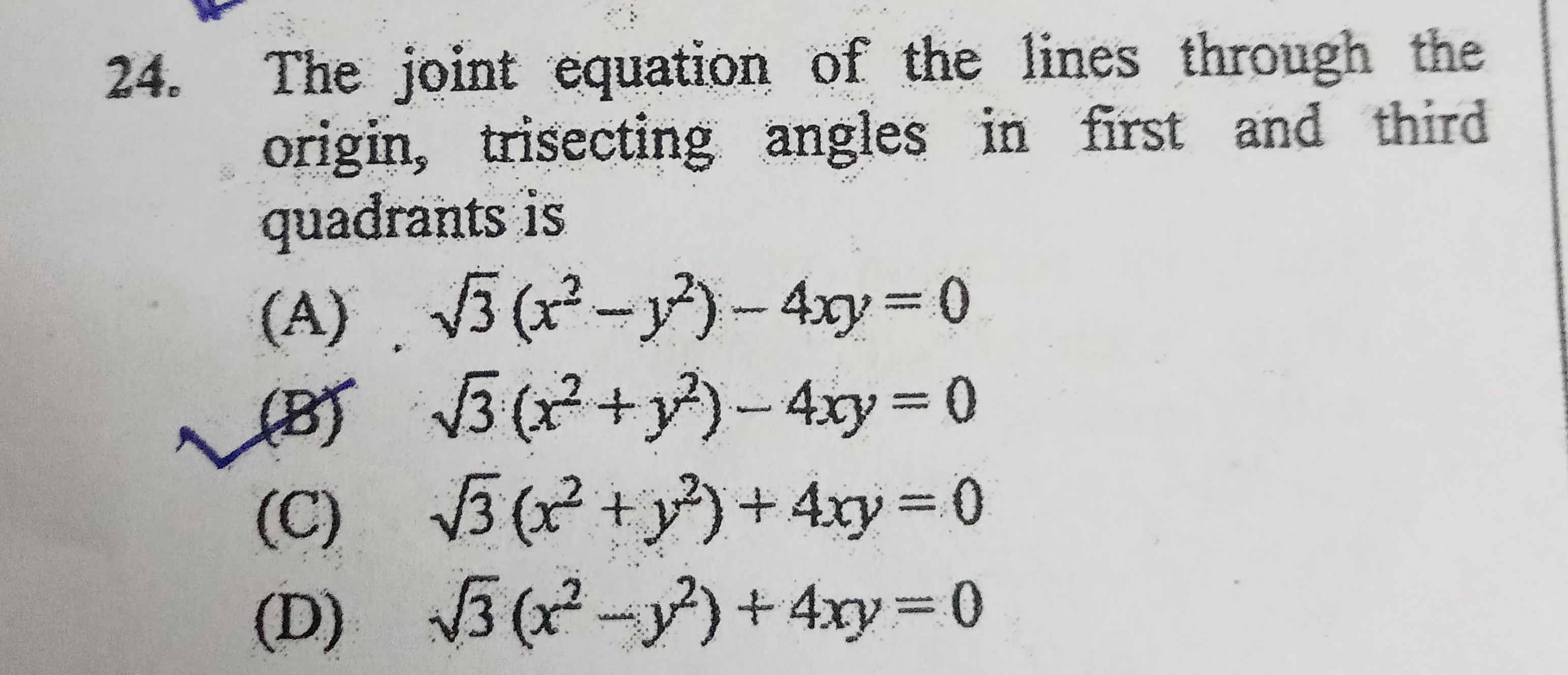
• A. $\sqrt{3}(x^2-y^2)-4xy=0$
• B. $\sqrt{3}(x^2+y^2)-4xy=0$
• C. $\sqrt{3}(x^2+y^2)+4xy=0$
• D. $\sqrt{3}(x^2-y^2)+4xy=0$

Answer 1

Answer: (B)

$\sqrt{3}(x^2+y^2)-4xy=0$

Answer 2

Solution:

The lines passing through the origin making angles of 30° and 60° in the first quadrant have slopes:

$$m_1 = \tan30^\circ = \frac{1}{\sqrt{3}}, \quad m_2 = \tan60^\circ = \sqrt{3}.$$

Their equations are:

$$y = \frac{x}{\sqrt{3}} \quad \Rightarrow \quad \sqrt{3}x - y = 0,$$ $$y = \sqrt{3}x \quad \Rightarrow \quad y - \sqrt{3}x = 0.$$

The joint equation is the product of these two factors:

$$(\sqrt{3}x - y)(y - \sqrt{3}x) = 0.$$

Notice that:

$$(\sqrt{3}x - y)(y - \sqrt{3}x) = -(\sqrt{3}x - y)^2.$$

To avoid a negative constant, rearrange the factors as:

$$(\sqrt{3}x - y)(\sqrt{3}y - x) = 0.$$

Expanding,

$$(\sqrt{3}x - y)(\sqrt{3}y - x) = \sqrt{3}\cdot\sqrt{3}xy - \sqrt{3}x^2 - \sqrt{3}y^2 + xy = 3xy - \sqrt{3}(x^2+y^2) + xy.$$

Combine like terms:

$$= 4xy - \sqrt{3}(x^2+y^2) = 0.$$

Multiplying both sides by -1 gives:

$$\sqrt{3}(x^2+y^2) - 4xy = 0.$$

Since lines through the origin in the first quadrant have corresponding lines in the third quadrant (their negatives), the same joint equation holds.

Core Explanation:

1. Find slopes using $\tan30^\circ$ and $\tan60^\circ$.
2. Write line equations through the origin.
3. Write the product of the factors to form the joint equation and simplify.