Question

The joint equation of the lines through the origin, trisecting angles in first and third quadrants is

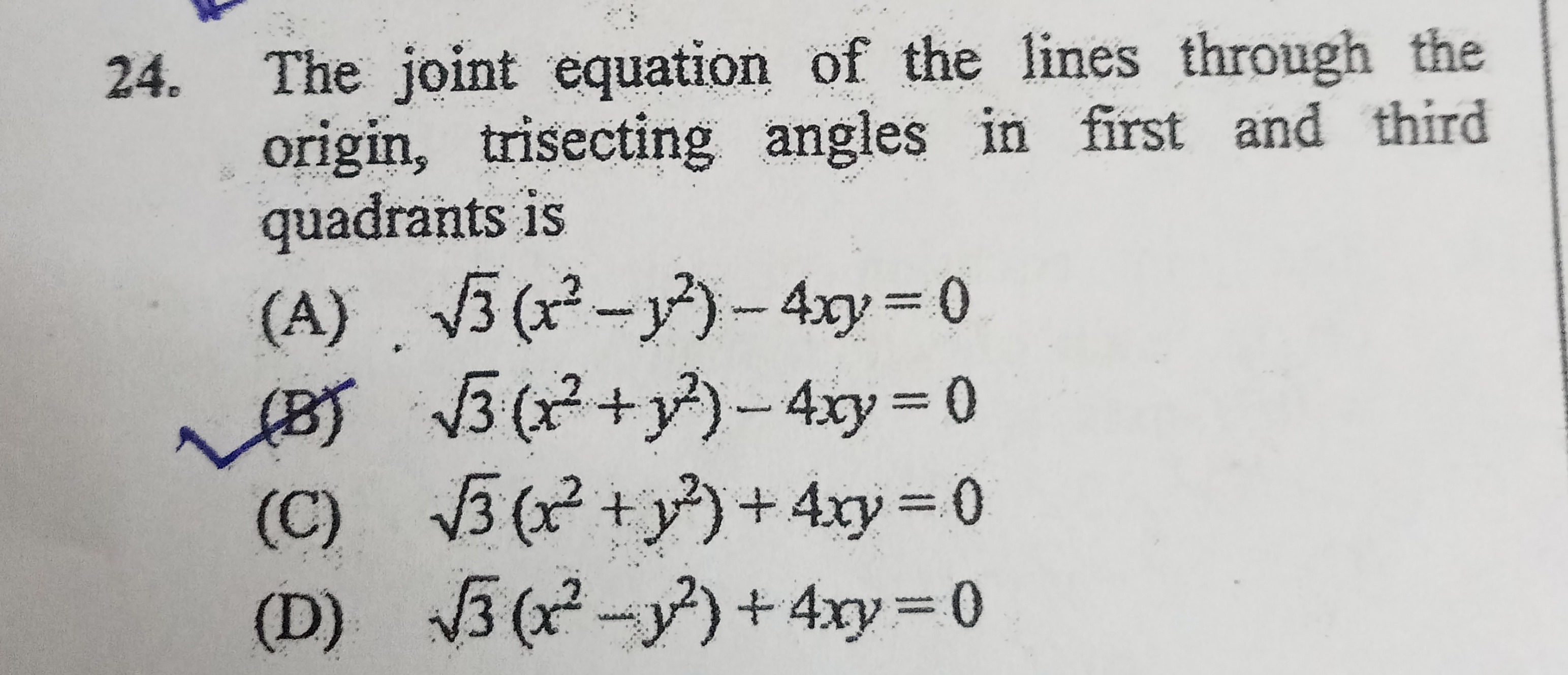
• A. $\sqrt{3} (x^2-y^2) - 4xy = 0$
• B. $\sqrt{3} (x^2+y^2) - 4xy = 0$
• C. $\sqrt{3} (x^2+y^2) + 4xy = 0$
• D. $\sqrt{3} (x^2-y^2) + 4xy = 0$

Answer 1

Answer: (B)

$\sqrt{3}(x^2+y^2) - 4xy = 0$

Answer 2

Solution:

Let the lines making angles $\theta$ with the x-axis have slopes $m = \tan \theta$. In the first quadrant, trisecting the right angle gives

$$\theta = 30^\circ \quad \text{and} \quad 60^\circ.$$

Thus, the slopes are

$$m_1 = \tan 30^\circ = \frac{1}{\sqrt{3}}, \quad m_2 = \tan 60^\circ = \sqrt{3}.$$

The equations of the lines through the origin are

$$y = \frac{1}{\sqrt{3}} x \quad \text{and} \quad y = \sqrt{3} x.$$

The combined (joint) equation is obtained by multiplying the individual equations:

$$\left(y - \frac{x}{\sqrt{3}}\right)\left(y - \sqrt{3}x\right) = 0.$$

Expanding,

$$y^2 - \left(\frac{1}{\sqrt{3}} + \sqrt{3}\right)xy + x^2 = 0.$$

Noting that

$$\frac{1}{\sqrt{3}} + \sqrt{3} = \frac{1 + 3}{\sqrt{3}} = \frac{4}{\sqrt{3}},$$

the equation becomes

$$y^2 - \frac{4}{\sqrt{3}}xy + x^2 = 0.$$

Multiplying through by $\sqrt{3}$ to clear the denominator:

$$\sqrt{3}y^2 - 4xy + \sqrt{3}x^2 = 0,$$

or equivalently,

$$\sqrt{3}(x^2 + y^2) - 4xy = 0.$$

Core Explanation:

Find slopes $m=\tan30^\circ$ and $m=\tan60^\circ$, write line equations through the origin, multiply, and simplify.