Question

The joint equation of the lines through the origin, trisecting angles in first and third quadrants is

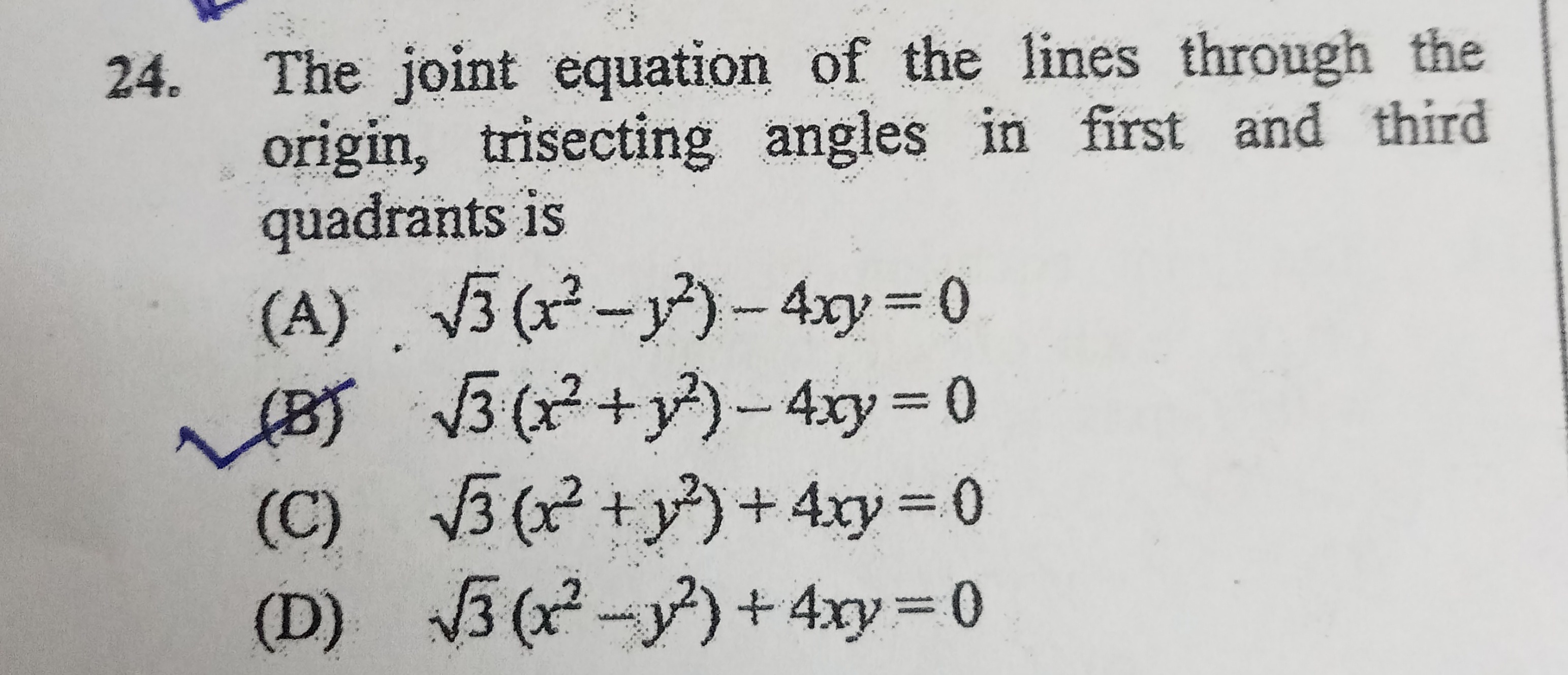
• A. $\sqrt{3}(x^2-y^2)-4xy=0$
• B. $\sqrt{3}(x^2+y^2)-4xy=0$
• C. $\sqrt{3}(x^2+y^2)+4xy=0$
• D. $\sqrt{3}(x^2-y^2)+4xy=0$

Answer 1

Answer: (B)

Option (B)

Answer 2

The lines that trisect the angles in the first and third quadrants have slopes corresponding to 30° and 60°. Their equations are:

For 30°: $y = \frac{1}{\sqrt{3}}x \Rightarrow \sqrt{3}x - y = 0$

For 60°: $y = \sqrt{3}x \Rightarrow x - \sqrt{3}y = 0$

The joint equation is the product of the two:

$$(\sqrt{3}x - y)(x - \sqrt{3}y)=0$$

Expanding:

$$\sqrt{3}x^2 - \sqrt{3}^2xy - xy + \sqrt{3}y^2 = \sqrt{3}x^2 - 3xy - xy + \sqrt{3}y^2 = \sqrt{3}x^2 - 4xy + \sqrt{3}y^2 = 0$$

Rewriting this gives:

$$\sqrt{3}(x^2+y^2) - 4xy= 0$$

Thus, the correct option is: Option (B)