Question

The joint equation of the lines through the origin, trisecting angles in first and third quadrants is

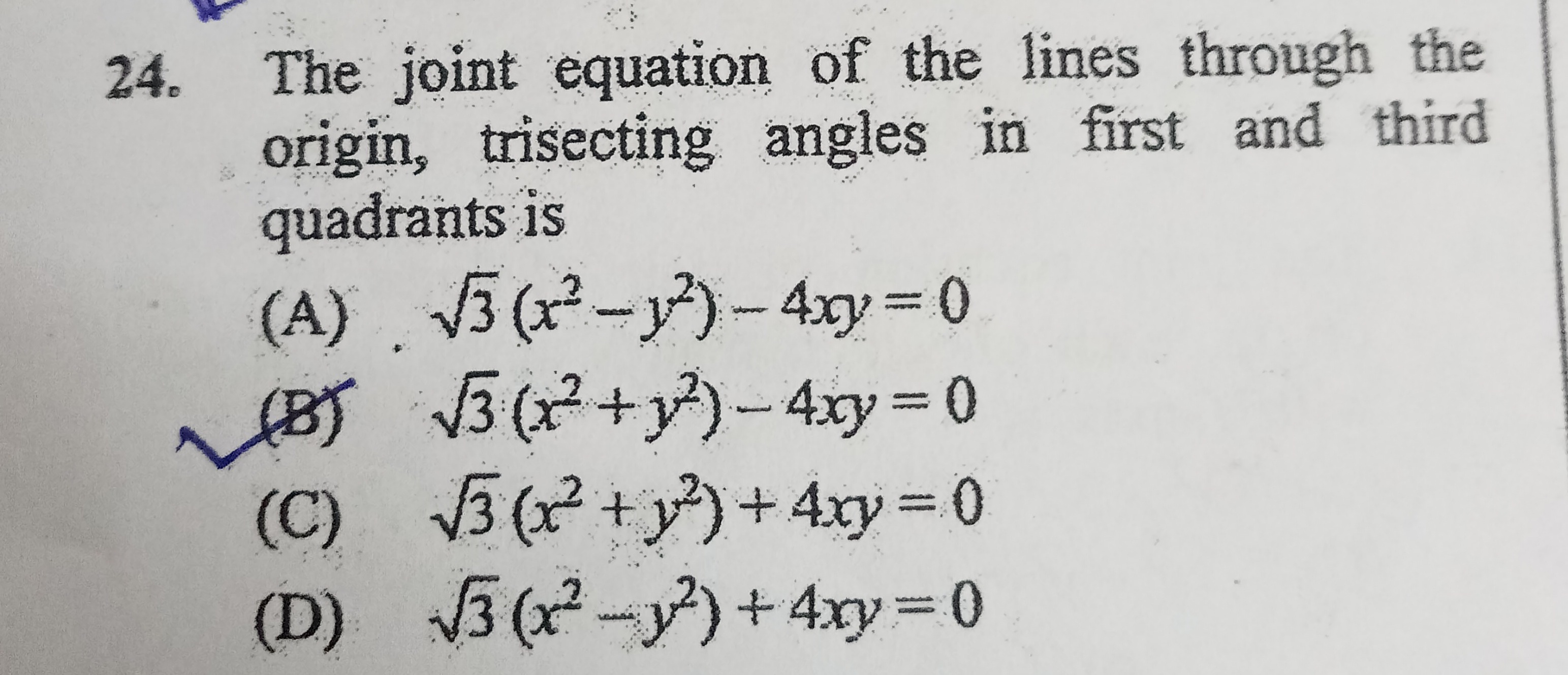
• A. $\sqrt{3}(x^2-y^2)-4xy=0$
• B. $\sqrt{3}(x^2+y^2)-4xy=0$
• C. $\sqrt{3}(x^2+y^2)+4xy=0$
• D. $\sqrt{3}(x^2-y^2)+4xy=0$

Answer 1

Answer: (B)

$\sqrt{3}(x^2+y^2)-4xy=0$

Answer 2

Solution:

The lines trisecting the angles in the first and third quadrants make angles of 30° and 60° with the positive x-axis. Their equations are

$y = \tan 30^\circ\, x = \frac{1}{\sqrt{3}}x$ and $y = \tan 60^\circ\, x = \sqrt{3}x$.

In standard form, they are:

$x - \sqrt{3}y = 0$ and $\sqrt{3}x - y = 0$.

The combined (joint) equation is the product:

$(x - \sqrt{3}y)(\sqrt{3}x - y) = 0$.

Expanding:

$(x)(\sqrt{3}x) - x\cdot y - \sqrt{3}y\cdot \sqrt{3}x + \sqrt{3}y\cdot y = \sqrt{3}x^2 - xy - 3xy + \sqrt{3}y^2 = \sqrt{3}x^2 - 4xy + \sqrt{3}y^2 = 0$.

This is equivalent to:

$\sqrt{3}(x^2 + y^2) - 4xy= 0$.

Thus, the correct option is (B).

---

Core Explanation (Minimal):

• Lines: $y=\frac{1}{\sqrt{3}}x$ and $y=\sqrt{3}x$.
• Joint Equation: $(x-\sqrt{3}y)(\sqrt{3}x-y)=0$ which expands to $\sqrt{3}x^2-4xy+\sqrt{3}y^2=0$.
• Rewrite as: $\sqrt{3}(x^2+y^2)-4xy=0$.