Question

One mole of an ideal monoatomic gas undergoes expansion along a straight line on P–V curve from initial state A(3L, 8 atm) to final state B(7.5 L, 2 atm). Calculate q for the above process in L atm

Answer 1

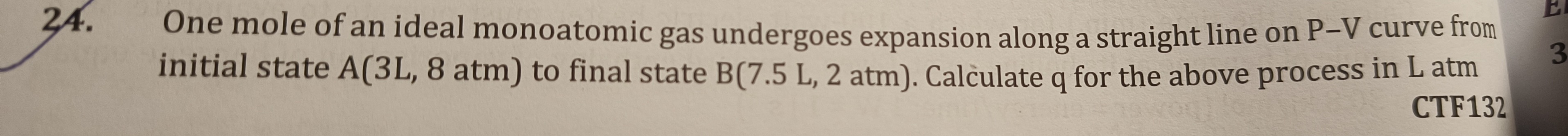
9.0 L atm

Answer 2

The problem asks to calculate the heat (q) for a process involving one mole of an ideal monoatomic gas expanding along a straight line on a P-V curve.

1. Calculate the work done (w) by the system: The process is a straight line on the P-V curve from state A(3L, 8 atm) to state B(7.5 L, 2 atm). The work done by the system ($w_{by\_system}$) is the area under the P-V curve. This area forms a trapezium. The formula for the area of a trapezium is $\frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$. Here, the parallel sides are the initial and final pressures ($P_1 = 8 \text{ atm}$, $P_2 = 2 \text{ atm}$), and the height is the change in volume ($V_2 - V_1 = 7.5 \text{ L} - 3 \text{ L}$).

$w_{by\_system} = \frac{1}{2}(P_1 + P_2)(V_2 - V_1)$ $w_{by\_system} = \frac{1}{2}(8 \text{ atm} + 2 \text{ atm})(7.5 \text{ L} - 3 \text{ L})$ $w_{by\_system} = \frac{1}{2}(10 \text{ atm})(4.5 \text{ L})$ $w_{by\_system} = 5 \times 4.5 \text{ L atm}$ $w_{by\_system} = 22.5 \text{ L atm}$

2. Calculate the change in internal energy ($\Delta U$): For an ideal gas, the change in internal energy depends only on the change in temperature: $\Delta U = nC_v\Delta T$. For a monoatomic ideal gas, the molar heat capacity at constant volume ($C_v$) is $\frac{3}{2}R$. So, $\Delta U = n \frac{3}{2}R\Delta T = \frac{3}{2} (nR T_2 - nR T_1)$. Using the ideal gas law, $PV = nRT$, we can substitute $nRT$ with $PV$: $\Delta U = \frac{3}{2}(P_2V_2 - P_1V_1)$

Calculate the initial and final PV products: $P_1V_1 = 8 \text{ atm} \times 3 \text{ L} = 24 \text{ L atm}$ $P_2V_2 = 2 \text{ atm} \times 7.5 \text{ L} = 15 \text{ L atm}$

Now, calculate $\Delta U$: $\Delta U = \frac{3}{2}(15 \text{ L atm} - 24 \text{ L atm})$ $\Delta U = \frac{3}{2}(-9 \text{ L atm})$ $\Delta U = -13.5 \text{ L atm}$

3. Apply the First Law of Thermodynamics: The First Law of Thermodynamics states that $\Delta U = q - w_{by\_system}$ (where $w_{by\_system}$ is work done by the system). Rearranging to find q: $q = \Delta U + w_{by\_system}$

Substitute the calculated values of $\Delta U$ and $w_{by\_system}$: $q = -13.5 \text{ L atm} + 22.5 \text{ L atm}$ $q = 9.0 \text{ L atm}$

The positive value of q indicates that heat is absorbed by the system during the process.