Question
Question: Let $S = \frac{1}{\sqrt{1}+\sqrt{3}} + \frac{1}{\sqrt{5}+\sqrt{7}} + \frac{1}{\sqrt{9}+\sqrt{11}} + ...
Let S=1+31+5+71+9+111+...+9997+99991, then
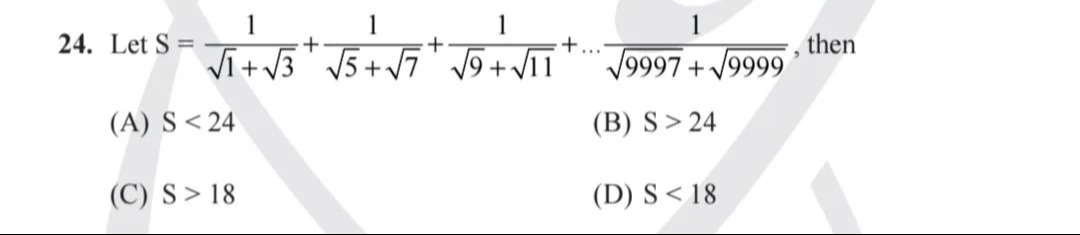
S < 24
S > 24
S > 18
S < 18
S > 24
Solution
The given sum is S=1+31+5+71+9+111+...+9997+99991. The general term of the series is Tn=4n−3+4n−11. There are 2500 terms in the sum.
First, rationalize the general term Tn: Tn=4n−3+4n−11=(4n−1+4n−3)(4n−1−4n−3)4n−1−4n−3=(4n−1)−(4n−3)4n−1−4n−3=24n−1−4n−3
So the sum S can be written as: S=∑n=1250024n−1−4n−3
Let f(x)=x. By the Mean Value Theorem, for a<b, there exists a c∈(a,b) such that b−af(b)−f(a)=f′(c). Here, let a=4n−3 and b=4n−1. Then b−a=2. So, 24n−1−4n−3=f′(cn) for some cn∈(4n−3,4n−1). Since f′(x)=2x1, we have Tn=2cn1. Since 4n−3<cn<4n−1, we can establish bounds for Tn: 24n−11<Tn<24n−31.
Summing these inequalities from n=1 to n=2500: ∑n=1250024n−11<S<∑n=1250024n−31
Using integral approximation, we find that 24.57075<S<25.24625.
From this range, we can conclude that S>24.
