Question

$\int \frac{\sin 2x + \sin 5x - \sin 3x}{\cos x + 1 - 2\sin^2 2x}dx$

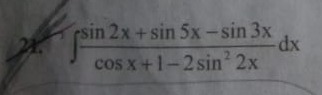
Answer 1

-2cos x + C

Answer 2

Step 1. Simplify the Numerator

We start with the numerator:

$$\sin 2x + \sin 5x - \sin 3x.$$

Combine $\sin 2x - \sin 3x$ using the identity:

$$\sin A - \sin B = 2\cos\frac{A+B}{2}\sin\frac{A-B}{2},$$

with $A=2x$ and $B=3x$:

$$\sin 2x - \sin 3x = 2\cos\frac{2x+3x}{2}\sin\frac{2x-3x}{2} = 2\cos\frac{5x}{2}\sin\left(-\frac{x}{2}\right) = -2\cos\frac{5x}{2}\sin\frac{x}{2}.$$

Thus, the numerator becomes:

$$\sin 5x -2\cos\frac{5x}{2}\sin\frac{x}{2}.$$

Now, write $\sin 5x$ in terms of half-angles:

$$\sin 5x = 2\sin\frac{5x}{2}\cos\frac{5x}{2}.$$

So,

$$\sin 5x -2\cos\frac{5x}{2}\sin\frac{x}{2} = 2\cos\frac{5x}{2}\left[\sin\frac{5x}{2} -\sin\frac{x}{2}\right].$$

Use the identity again on $\sin\frac{5x}{2} -\sin\frac{x}{2}$:

$$\sin A - \sin B = 2\cos\frac{A+B}{2}\sin\frac{A-B}{2},$$

with $A=\frac{5x}{2},\; B=\frac{x}{2}$, we get:

$$\sin\frac{5x}{2}-\sin\frac{x}{2} = 2\cos\frac{5x/2+x/2}{2}\sin\frac{5x/2-x/2}{2} = 2\cos\frac{3x}{2}\sin x.$$

Thus, the numerator simplifies to:

$$2\cos\frac{5x}{2}\cdot 2\cos\frac{3x}{2}\sin x = 4\sin x \cos\frac{5x}{2}\cos\frac{3x}{2}.$$

Step 2. Simplify the Denominator

The denominator is:

$$\cos x + 1 - 2\sin^2 2x.$$

Rewrite $2\sin^2 2x$ using the identity:

$$\sin^2\theta = \frac{1-\cos 2\theta}{2},$$

with $\theta=2x$:

$$2\sin^2 2x = 2\cdot\frac{1-\cos4x}{2} = 1-\cos4x.$$

Thus,

$$\cos x+1-2\sin^2 2x = \cos x + 1 - (1-\cos4x) = \cos x + \cos4x.$$

Now, use the sum-to-product formula:

$$\cos A+\cos B = 2\cos\frac{A+B}{2}\cos\frac{A-B}{2},$$

with $A=x$ and $B=4x$:

$$\cos x+\cos4x = 2\cos\frac{x+4x}{2}\cos\frac{x-4x}{2} = 2\cos\frac{5x}{2}\cos\left(-\frac{3x}{2}\right) = 2\cos\frac{5x}{2}\cos\frac{3x}{2}.$$

Step 3. Write the Integral

Substitute the simplified numerator and denominator into the integral:

$$\int \frac{4\sin x \cos\frac{5x}{2}\cos\frac{3x}{2}}{2\cos\frac{5x}{2}\cos\frac{3x}{2}}\,dx = \int \frac{4\sin x}{2}\,dx = \int 2\sin x\,dx.$$

Step 4. Integrate

$$\int 2\sin x\,dx = -2\cos x + C.$$