Question

For the combustion of 1 mole of liquid benzene at 298 K, the heat of reaction at constant pressure is -3268 kJ mol⁻¹. What is heat of combustion at constant volume? (R = 8.314 × 10⁻³ kJ K⁻¹ mol⁻¹)

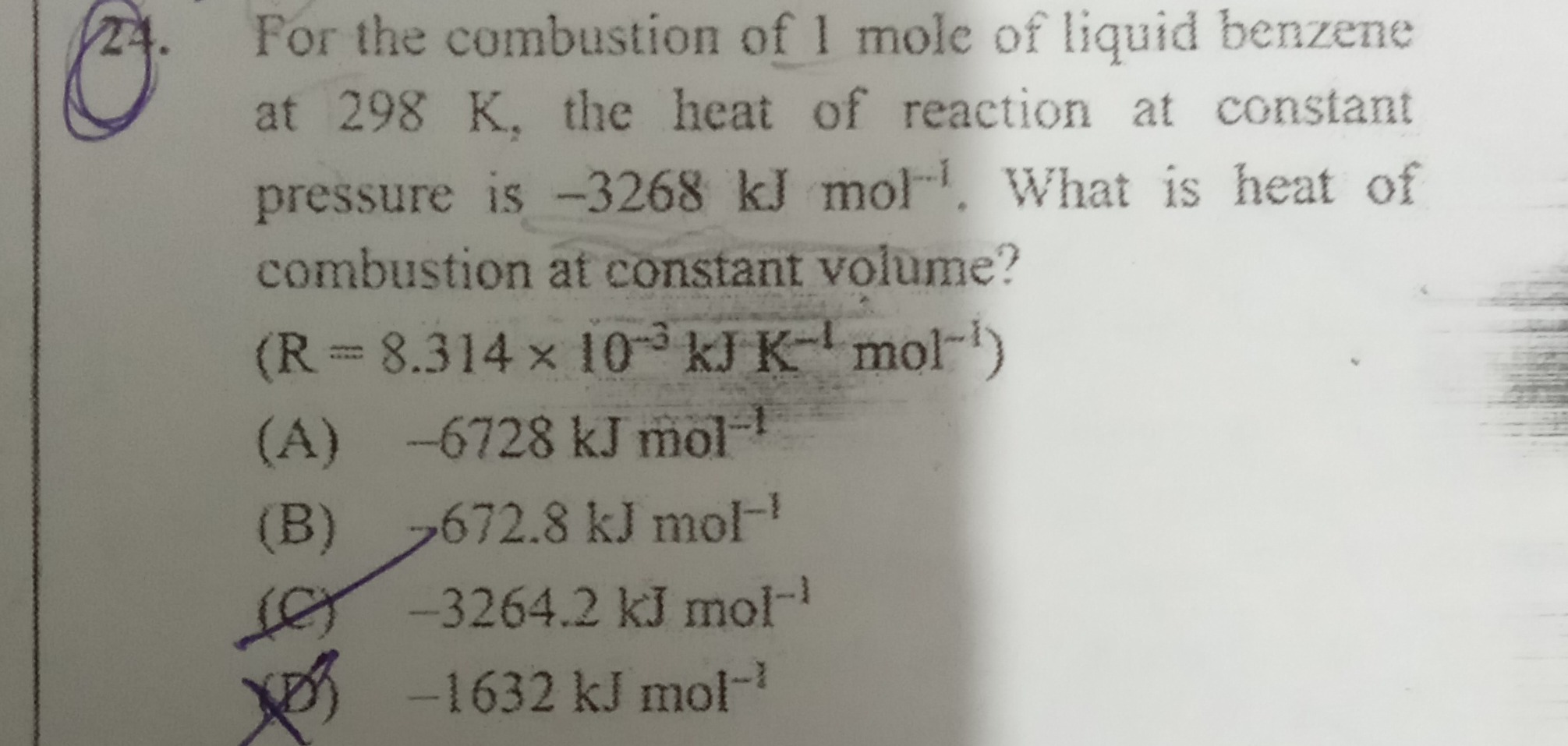
• A. -6728 kJ mol⁻¹
• B. -672.8 kJ mol⁻¹
• C. -3264.2 kJ mol⁻¹
• D. -1632 kJ mol⁻¹

Answer 1

Answer: (C)

-3264.2 kJ mol⁻¹

Answer 2

For a reaction, the relation between the heat at constant pressure ($\Delta H$) and constant volume ($\Delta U$) is given by

$$\Delta U = \Delta H - \Delta n_g\,RT$$

For the combustion of liquid benzene, the balanced reaction is:

$$\mathrm{C_6H_6(l)} + \frac{15}{2}\,\mathrm{O_2(g)} \rightarrow 6\,\mathrm{CO_2(g)} + 3\,\mathrm{H_2O(l)}$$

Here, only gaseous species count when calculating $\Delta n_g$:

• Moles of gas in reactants = $\frac{15}{2} = 7.5$
• Moles of gas in products = $6$ (since water is liquid)

Thus,

$$\Delta n_g = 6 - 7.5 = -1.5$$

Given:

$$\Delta H = -3268 \text{ kJ/mol}, \quad R = 8.314\times10^{-3}\,\text{kJ/K/mol}, \quad T = 298\,\text{K}$$

Then,

$$\Delta U = -3268 - (-1.5)(8.314\times10^{-3})(298)$$

Calculate the term:

$$RT = 8.314\times10^{-3}\times298 \approx 2.478\,\text{kJ/mol}$$ $$1.5\times RT \approx 1.5\times 2.478 \approx 3.717\,\text{kJ/mol}$$

Finally,

$$\Delta U \approx -3268 + 3.717 \approx -3264.283\,\text{kJ/mol} \approx -3264.2\,\text{kJ/mol}$$