Question

24. Find the value of 'p' for which the quadratic equ $p(x-4)(x-2) + (x-1)^2 = 0$ has real and equal roots.

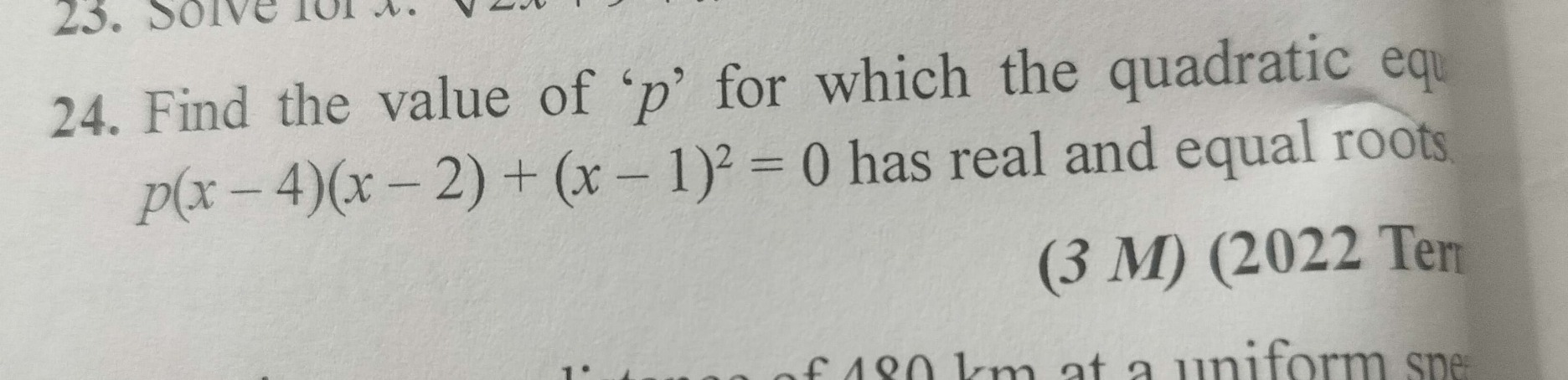
Answer 1

p=0 and p=3

Answer 2

Explanation:

1. Expand the expression:
     $p(x-4)(x-2) + (x-1)^2 = p(x^2-6x+8) + (x^2-2x+1)$
     $= (p+1)x^2 - (6p+2)x + (8p+1)$

2. For equal roots, set the discriminant to zero:
     $\Delta = (6p+2)^2 - 4(p+1)(8p+1)=0$

3. Compute and simplify the discriminant:
     $(6p+2)^2 = 36p^2+24p+4$
     $4(p+1)(8p+1) = 32p^2+36p+4$
     Thus,
     $\Delta = (36p^2+24p+4) - (32p^2+36p+4) = 4p^2 - 12p = 4p(p-3)=0$

4. Solving $4p(p-3)=0$ gives:
     $p=0$ or $p=3$.

Answer:
The quadratic has real and equal roots for $p=0$ and $p=3$.