Question

During a number of complete cycles, a reversible engine (shown by a circle) absorbs 1200 joule from reservoir at 400 K and performs 200 joule of mechanical work then:

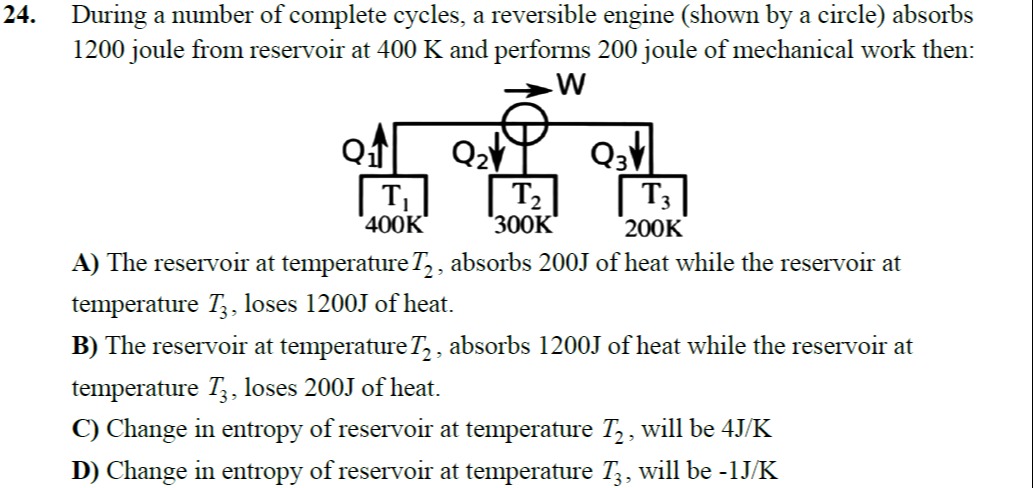
• A. The reservoir at temperature $T_2$, absorbs 200J of heat while the reservoir at temperature $T_3$, loses 1200J of heat.
• B. The reservoir at temperature $T_2$, absorbs 1200J of heat while the reservoir at temperature $T_3$, loses 200J of heat.
• C. Change in entropy of reservoir at temperature $T_2$, will be 4J/K
• D. Change in entropy of reservoir at temperature $T_3$, will be -1J/K

Answer 1

Answer: (C)

C

Answer 2

The problem describes a reversible engine operating in a cycle with three heat reservoirs at temperatures $T_1 = 400 \, \text{K}$, $T_2 = 300 \, \text{K}$, and $T_3 = 200 \, \text{K}$. The engine absorbs $Q_1 = 1200 \, \text{J}$ from the reservoir at $T_1 = 400 \, \text{K}$ and performs work $W = 200 \, \text{J}$. Let $Q_2$ be the heat exchanged with the reservoir at $T_2$, and $Q_3$ be the heat exchanged with the reservoir at $T_3$. According to the first law of thermodynamics for a complete cycle, the net heat absorbed equals the net work done:

$Q_1 + Q_2 + Q_3 = W$ $1200 + Q_2 + Q_3 = 200$ $Q_2 + Q_3 = -1000 \, \text{J}$

(Note: $Q_i$ is positive if absorbed by the engine and negative if rejected by the engine).

Since the engine is reversible and operates in a cycle, the total change in entropy of the system (engine + reservoirs) is zero. The change in entropy of the engine over a cycle is zero. The total change in entropy of the reservoirs is zero. The change in entropy of a reservoir at temperature $T$ that exchanges heat $Q$ with the engine is $\Delta S = -\frac{Q}{T}$ (where $Q$ is the heat absorbed by the engine from the reservoir).

So, for the three reservoirs, the total change in entropy is:

$\Delta S_{total} = \Delta S_1 + \Delta S_2 + \Delta S_3 = -\frac{Q_1}{T_1} - \frac{Q_2}{T_2} - \frac{Q_3}{T_3} = 0$ $\frac{Q_1}{T_1} + \frac{Q_2}{T_2} + \frac{Q_3}{T_3} = 0$ $\frac{1200}{400} + \frac{Q_2}{300} + \frac{Q_3}{200} = 0$ $3 + \frac{Q_2}{300} + \frac{Q_3}{200} = 0$ $\frac{Q_2}{300} + \frac{Q_3}{200} = -3$

We have a system of two linear equations:

1. $Q_2 + Q_3 = -1000$
2. $\frac{Q_2}{300} + \frac{Q_3}{200} = -3$

From equation (1), $Q_3 = -1000 - Q_2$. Substitute into equation (2): $\frac{Q_2}{300} + \frac{-1000 - Q_2}{200} = -3$ Multiply by 600: $2 Q_2 + 3 (-1000 - Q_2) = -3 \times 600$ $2 Q_2 - 3000 - 3 Q_2 = -1800$ $-Q_2 = -1800 + 3000$ $-Q_2 = 1200$ $Q_2 = -1200 \, \text{J}$

Now find $Q_3$: $Q_3 = -1000 - Q_2 = -1000 - (-1200) = -1000 + 1200 = 200 \, \text{J}$

So, the engine absorbs $Q_1 = 1200 \, \text{J}$ from $T_1 = 400 \, \text{K}$, rejects $Q_2 = 1200 \, \text{J}$ to $T_2 = 300 \, \text{K}$ (since $Q_2 = -1200$), and absorbs $Q_3 = 200 \, \text{J}$ from $T_3 = 200 \, \text{K}$.

Change in entropy of reservoir at temperature $T_2$ is $\Delta S_2 = \frac{\text{Heat absorbed by reservoir}}{T_2} = \frac{1200}{300} = 4 \, \text{J/K}$.