Question

Derivative of $\log_e 2 (\log x)$ with respect to $x$ is

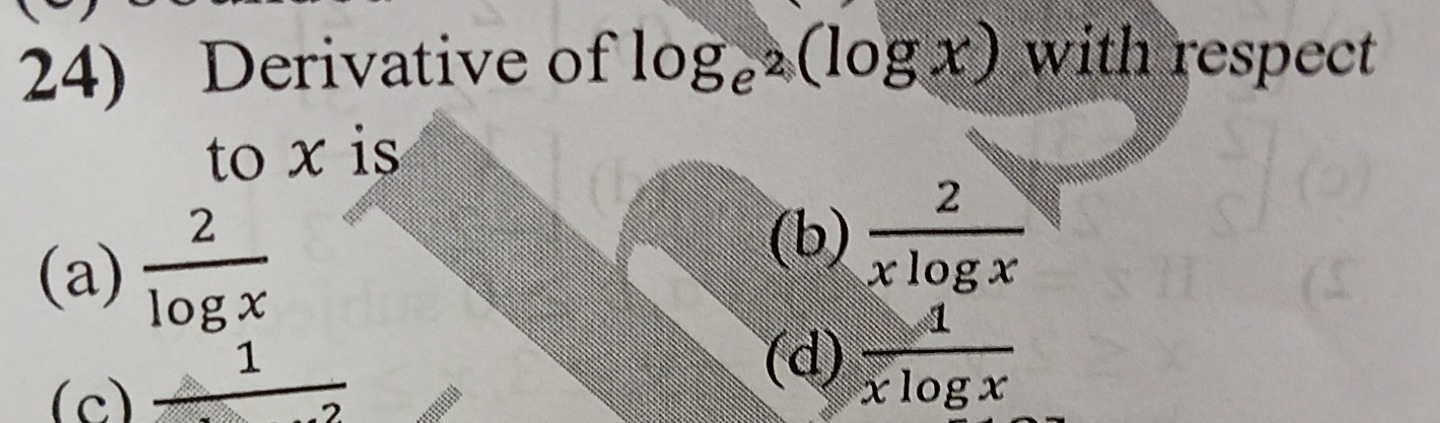
• A. $\frac{2}{\log x}$
• B. $\frac{2}{x \log x}$
• C. $\frac{1}{x^2}$
• D. $\frac{1}{x \log x}$

Answer 1

Answer: (D)

$\frac{1}{x \log x}$

Answer 2

Interpreting the function as

$$f(x)=\ln\bigl(2\ln x\bigr),$$

we can write

$$f(x)=\ln 2 + \ln(\ln x).$$

Differentiating, the constant term $\ln2$ vanishes, so we have

$$f'(x)=\frac{d}{dx}\ln(\ln x)=\frac{1}{\ln x}\cdot\frac{1}{x}=\frac{1}{x\ln x}.$$

Thus, the correct answer is Option (d).