Question

The general solution of differential equation

$e^{2y}(\frac{dy}{dx})=3^x$ is

(where C is a constant of integration.)

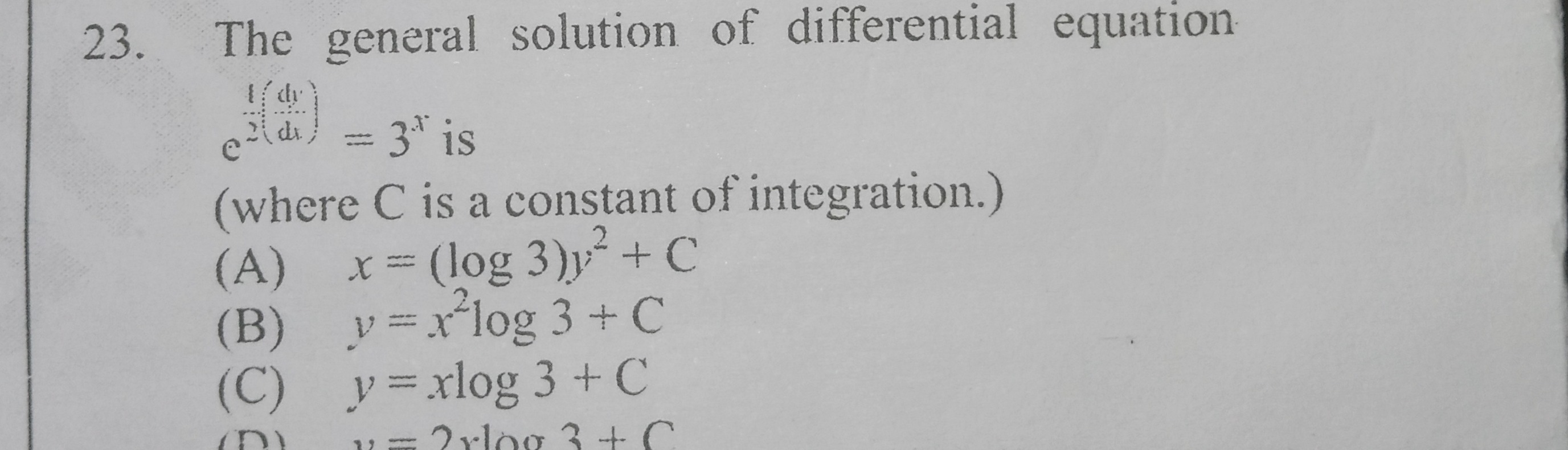
• A. $x = (\log 3)y^2 + C$
• B. $y = x^2\log 3 + C$
• C. $y = x\log 3 + C$

Answer 1

There is likely an error in the question or options. Assuming the intended ODE was $\frac{dy}{dx} = \ln 3$, the solution is $y = x \ln 3 + C$.

Answer 2

The given differential equation is $e^{2y}(\frac{dy}{dx})=3^x$. This is a first-order separable differential equation. We can separate the variables $y$ and $x$ as follows: $e^{2y} dy = 3^x dx$

Now, integrate both sides of the equation: $\int e^{2y} dy = \int 3^x dx$

For the left side, let $u = 2y$, so $du = 2 dy$, which means $dy = \frac{1}{2} du$. $\int e^{2y} dy = \int e^u \frac{1}{2} du = \frac{1}{2} \int e^u du = \frac{1}{2} e^u + C_1 = \frac{1}{2} e^{2y} + C_1$.

For the right side, the integral of $a^x$ is $\frac{a^x}{\ln a} + C$. $\int 3^x dx = \frac{3^x}{\ln 3} + C_2$.

Equating the results of the integration: $\frac{1}{2} e^{2y} + C_1 = \frac{3^x}{\ln 3} + C_2$ $\frac{1}{2} e^{2y} = \frac{3^x}{\ln 3} + (C_2 - C_1)$ Let $C = C_2 - C_1$ be the constant of integration. The general solution is $\frac{1}{2} e^{2y} = \frac{3^x}{\ln 3} + C$.

However, this solution doesn't match any of the provided options. It is highly likely that there's an error in the original question or the provided options.

If we assume the intended differential equation was $\frac{dy}{dx} = \ln 3$, then: $\int dy = \int \ln 3 dx$ $y = x \ln 3 + C$

This matches option (C), assuming $\log 3 = \ln 3$.