Question

Let k be a positive real number such that $\frac{1}{k+a} + \frac{1}{k+b} + \frac{1}{k+c} < 1$ for any positive real numbers a, b and c with abc = 1. Then the least integral value of k is equal to

Answer 1

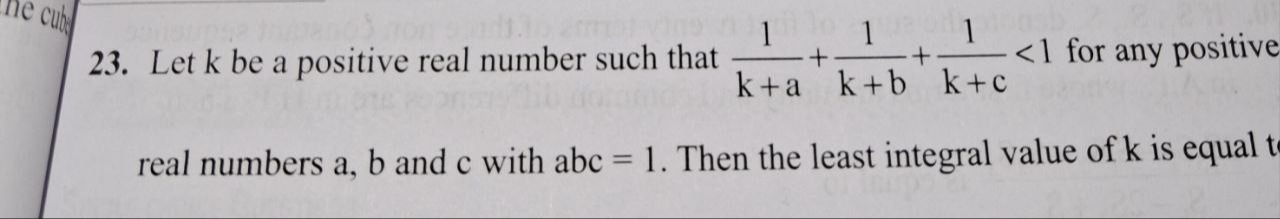
3

Answer 2

The problem asks for the least integral value of a positive real number $k$ such that the inequality $\frac{1}{k+a} + \frac{1}{k+b} + \frac{1}{k+c} < 1$ holds for any positive real numbers $a, b, c$ with $abc = 1$.

We need to find the smallest integer $k$ that satisfies this condition.

Step 1: Determine the necessary conditions for k.

We consider specific cases for $a, b, c$ that satisfy $abc=1$.

• Case 1: $a=b=c=1$

  If $a=b=c=1$, then $abc=1$ is satisfied. Substituting these values into the inequality: $\frac{1}{k+1} + \frac{1}{k+1} + \frac{1}{k+1} < 1$ $\frac{3}{k+1} < 1$ Since $k$ is a positive real number, $k+1$ is positive. We can multiply both sides by $k+1$ without changing the inequality direction: $3 < k+1$ $k > 2$

• Case 2: Consider a limit where one variable becomes very large and the others become very small.

  Let $a = N^2$, $b = \frac{1}{N}$, $c = \frac{1}{N}$. As $N \to \infty$, $a \to \infty$, $b \to 0^+$, and $c \to 0^+$. Also, $abc = N^2 \cdot \frac{1}{N} \cdot \frac{1}{N} = 1$ is always satisfied. Substitute these into the inequality: $\frac{1}{k+N^2} + \frac{1}{k+1/N} + \frac{1}{k+1/N} < 1$ Now, consider the limit as $N \to \infty$: $\lim_{N \to \infty} \left( \frac{1}{k+N^2} + \frac{1}{k+1/N} + \frac{1}{k+1/N} \right)$ $= 0 + \frac{1}{k+0} + \frac{1}{k+0} = \frac{1}{k} + \frac{1}{k} = \frac{2}{k}$ Since the inequality must hold for all $a,b,c$, it must hold for the limit of this sequence. Therefore: $\frac{2}{k} \le 1$ Since $k$ is positive, we can multiply by $k$: $2 \le k$

Combining the conditions from Case 1 ($k>2$) and Case 2 ($k \ge 2$), we must have $k>2$. Since $k$ is an integer, the least integral value of $k$ must be $3$.

Step 2: Verify that $k=3$ satisfies the inequality for all $a,b,c > 0$ with $abc=1$.

We need to prove that $\frac{1}{3+a} + \frac{1}{3+b} + \frac{1}{3+c} < 1$ for all $a,b,c > 0$ with $abc=1$. To prove this, we can clear the denominators. Multiply both sides by $(3+a)(3+b)(3+c)$: $(3+b)(3+c) + (3+a)(3+c) + (3+a)(3+b) < (3+a)(3+b)(3+c)$ Expand the terms:

Left Hand Side (LHS): $(9+3b+3c+bc) + (9+3a+3c+ac) + (9+3a+3b+ab)$ $= 27 + 6a + 6b + 6c + ab + bc + ca$ $= 27 + 6(a+b+c) + (ab+bc+ca)$

Right Hand Side (RHS): $(9+3a+3b+ab)(3+c)$ $= 27 + 9c + 9a + 3ac + 9b + 3bc + 3ab + abc$ $= 27 + 9(a+b+c) + 3(ab+bc+ca) + abc$ Since $abc=1$, substitute this into the RHS: $\text{RHS} = 27 + 9(a+b+c) + 3(ab+bc+ca) + 1$ $= 28 + 9(a+b+c) + 3(ab+bc+ca)$

Now, the inequality becomes: $27 + 6(a+b+c) + (ab+bc+ca) < 28 + 9(a+b+c) + 3(ab+bc+ca)$ Rearrange the terms by moving all terms to the right side: $0 < (28-27) + (9-6)(a+b+c) + (3-1)(ab+bc+ca)$ $0 < 1 + 3(a+b+c) + 2(ab+bc+ca)$ Since $a,b,c$ are positive real numbers, $a+b+c$ is positive and $ab+bc+ca$ is positive. Therefore, $1 + 3(a+b+c) + 2(ab+bc+ca)$ is always positive. This proves that the inequality $\frac{1}{3+a} + \frac{1}{3+b} + \frac{1}{3+c} < 1$ holds true for all positive $a,b,c$ with $abc=1$.

Conclusion:

We found that $k$ must be strictly greater than 2, and we proved that $k=3$ satisfies the condition. Therefore, the least integral value of $k$ is 3.