Solveeit Logo
Login

Question

Question: 23. If $y = \sqrt{(x-sinx) + \sqrt{(x-sinx) + \sqrt{(x-sinx).........}}}$ then $\frac{dy}{dx} =$...

  1. If y=(x−sinx)+(x−sinx)+(x−sinx).........y = \sqrt{(x-sinx) + \sqrt{(x-sinx) + \sqrt{(x-sinx).........}}}

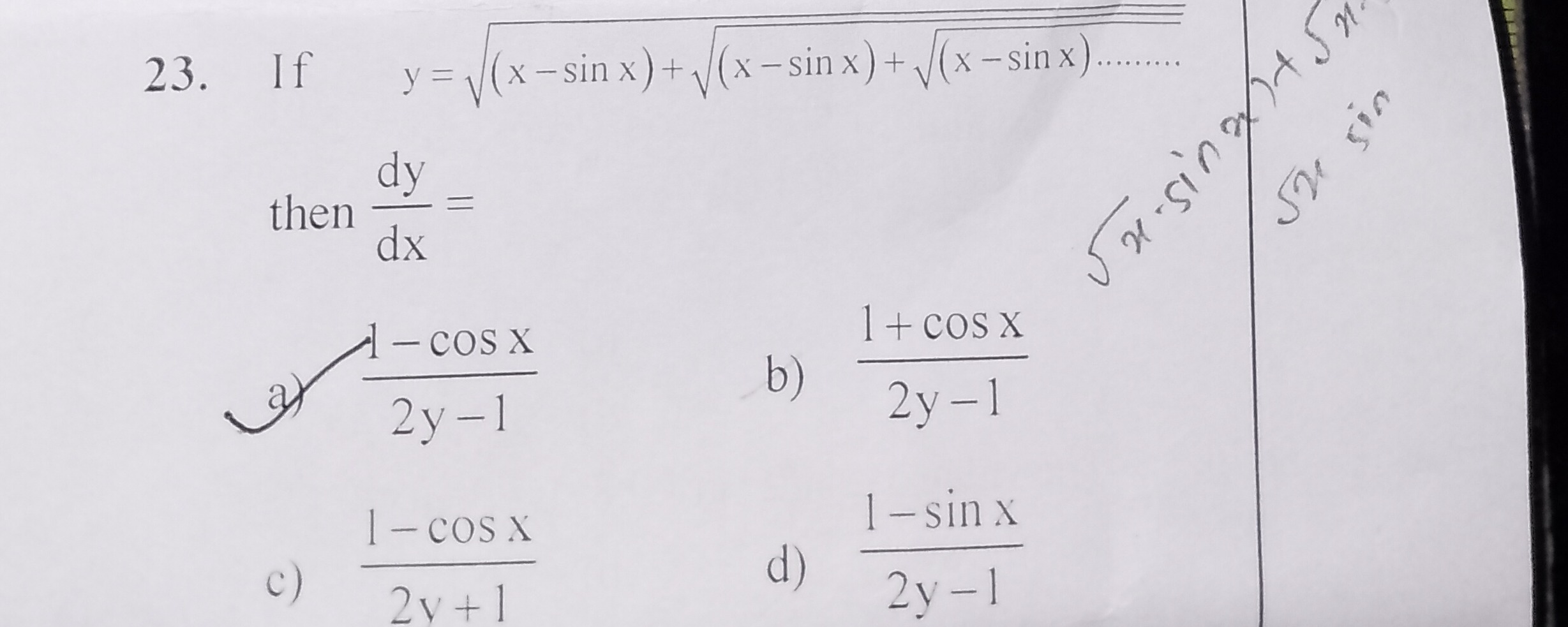
then dydx=\frac{dy}{dx} =

A

1−cosx2y−1\frac{1-cosx}{2y-1}

B

1+cosx2y−1\frac{1+cosx}{2y-1}

C

1−cosx2y+1\frac{1-cosx}{2y+1}

D

1−sinx2y−1\frac{1-sinx}{2y-1}

Answer

a) 1−cosx2y−1\frac{1-cosx}{2y-1}

Explanation

Solution

The expression is given by:

y=(x−sin⁡x)+(x−sin⁡x)+(x−sin⁡x)+⋯y = \sqrt{(x-\sin x) + \sqrt{(x-\sin x)+\sqrt{(x-\sin x)+\cdots}}}

Since the radical repeats, we have:

y=(x−sin⁡x)+yy = \sqrt{(x-\sin x) + y}

Squaring both sides gives:

y2=(x−sin⁡x)+y⟹y2−y−(x−sin⁡x)=0y^2 = (x-\sin x) + y \quad \Longrightarrow \quad y^2 - y - (x-\sin x)=0

Differentiating implicitly with respect to xx:

2ydydx−dydx−(1−cos⁡x)=02y\frac{dy}{dx} - \frac{dy}{dx} - (1-\cos x) = 0 (2y−1)dydx=1−cos⁡x(2y-1)\frac{dy}{dx} = 1-\cos x

Thus,

dydx=1−cos⁡x2y−1\frac{dy}{dx}=\frac{1-\cos x}{2y-1}