Question
Question: If $f_n(x) = \prod_{s=0}^{n-1}(2\cos(2^s x) - 1), n \ge 1$. Then which of the following is/are true-...
If fn(x)=∏s=0n−1(2cos(2sx)−1),n≥1. Then which of the following is/are true-
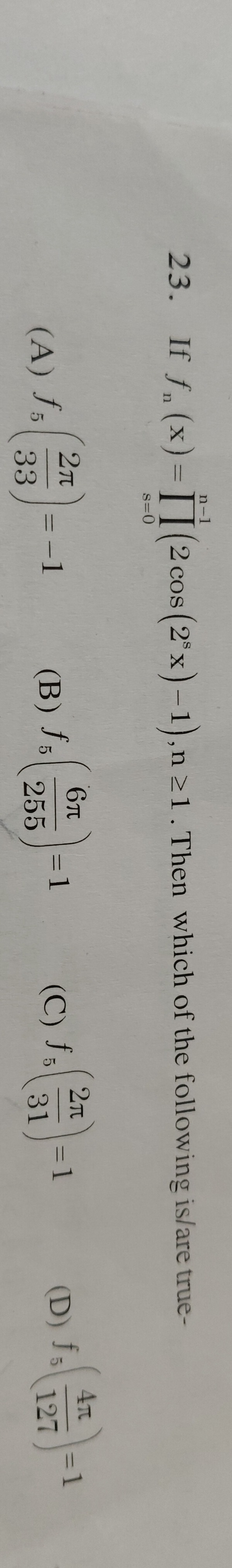
f5(332π)=−1
f5(2556π)=1
f5(312π)=1
f5(1274π)=1
C
Solution
Let fn(x)=∏s=0n−1(2cos(2sx)−1). We can simplify the general term 2cosθ−1 using complex exponentials. Let z=eiθ. Then 2cosθ−1=z+z−1−1=zz2−z+1. We know the identity z3+1=(z+1)(z2−z+1), so z2−z+1=z+1z3+1. Substituting this back, 2cosθ−1=z1z+1z3+1. Now, let θ=2sx. So z=ei2sx. The general term of the product becomes: 2cos(2sx)−1=ei2sx1ei2sx+1ei3⋅2sx+1.
Now, let's write out the product fn(x): fn(x)=∏s=0n−1(ei2sx1ei2sx+1ei3⋅2sx+1) fn(x)=∏s=0n−1ei2sx∏s=0n−1(ei2sx+1)∏s=0n−1(ei3⋅2sx+1).
Let's simplify the terms in the denominator:
- ∏s=0n−1ei2sx=eix∑s=0n−12s=eix(2n−1).
- ∏s=0n−1(ei2sx+1). We use the identity ∏k=0m−1(A2k+1)=A−1A2m−1. Here, A=eix and m=n. So, ∏s=0n−1(ei2sx+1)=eix−1(eix)2n−1=eix−1ei2nx−1. Combining these, the denominator of fn(x) is ei(2n−1)xeix−1ei2nx−1.
Now for the numerator: ∏s=0n−1(ei3⋅2sx+1). Let X=3x. This product is ∏s=0n−1(ei2sX+1)=eiX−1ei2nX−1=ei3x−1ei3⋅2nx−1.
So, the general formula for fn(x) is: fn(x)=ei(2n−1)xeix−1ei2nx−1ei3x−1ei3⋅2nx−1. This formula is valid as long as the denominators are non-zero. That means eix=1, ei3x=1, ei2nx=1.
Let's evaluate the options for n=5.
(C) f5(312π) Here n=5, x=312π. Denominator: ei(25−1)xeix−1ei25x−1=ei31xeix−1ei32x−1. 31x=31⋅312π=2π. So ei31x=1. 32x=32⋅312π=3164π=2π+312π. So ei32x=ei2π/31=eix. The denominator is 1⋅eix−1eix−1=1. (Since eix=1).
Numerator: ei3x−1ei3⋅25x−1=ei3x−1ei96x−1. 96x=96⋅312π=31192π=6π+316π. So ei96x=ei6π/31. 3x=3⋅312π=316π. So ei3x=ei6π/31. The numerator is ei6π/31−1ei6π/31−1=1. (Since ei6π/31=1).
So, f5(312π)=11=1. Option (C) states f5(312π)=1. So (C) is true.
