Question

Given the equation of the ellipse $\frac{(x-3)^2}{16}+\frac{(y+4)^2}{49}=1$, a parabola is such that its vertex is the lowest point of the ellipse and it passes through the ends of the minor axis of the ellipse. The equation of the parabola is in the form $16y=a(x-h)^2-k$. Determine the value of $(a+h+k)$.

Answer 1

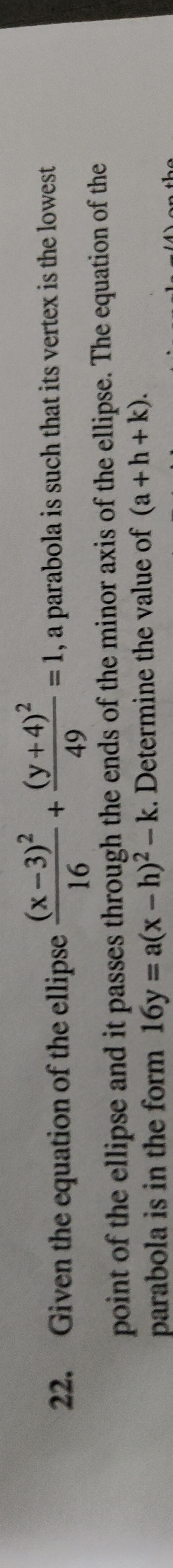
186

Answer 2

The ellipse has center $(3, -4)$, semi-major axis $a_e=7$ (vertical), and semi-minor axis $b_e=4$ (horizontal). The lowest point of the ellipse is $(3, -4-7) = (3, -11)$, which is the vertex of the parabola. The ends of the minor axis are $(3 \pm 4, -4)$, i.e., $(7, -4)$ and $(-1, -4)$. The parabola equation with vertex $(3, -11)$ is $y+11 = A(x-3)^2$. Substituting $(7, -4)$: $-4+11 = A(7-3)^2 \implies 7 = 16A \implies A = \frac{7}{16}$. The equation becomes $y+11 = \frac{7}{16}(x-3)^2$. Multiplying by 16: $16(y+11) = 7(x-3)^2 \implies 16y + 176 = 7(x-3)^2 \implies 16y = 7(x-3)^2 - 176$. Comparing with $16y=a(x-h)^2-k$, we have $a=7$, $h=3$, and $k=176$. Therefore, $a+h+k = 7+3+176 = 186$.