Question

A laser beam ($\lambda$ = 633 nm) has an power of 3 mW. What will be the pressure exerted on a surface by this beam if the cross sectional area is 3 $mm^2$. (Assume perfect reflection and normal incidence)

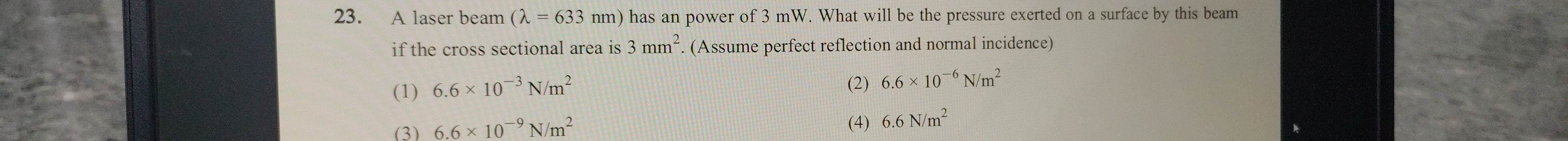
• A. 6.6 $\times 10^{-3} N/m^2$
• B. 6.6 $\times 10^{-6} N/m^2$
• C. 6.6 $\times 10^{-9} N/m^2$
• D. 6.6 $N/m^2$

Answer 1

Answer: (B)

6.6 $\times 10^{-6} N/m^2$

Answer 2

The pressure exerted by a laser beam on a perfectly reflecting surface at normal incidence is given by $P = 2I/c$, where $I$ is the intensity of the beam and $c$ is the speed of light. Intensity is calculated as power per unit area ($I = P_{power}/A$). Convert given power (3 mW) to Watts ($3 \times 10^{-3}$ W) and area (3 $mm^2$) to square meters ($3 \times 10^{-6}$ $m^2$). Calculate intensity $I = (3 \times 10^{-3}) / (3 \times 10^{-6}) = 10^3$ $W/m^2$. Then, calculate pressure $P = (2 \times 10^3) / (3 \times 10^8) = (2/3) \times 10^{-5} \approx 6.67 \times 10^{-6}$ $N/m^2$.