Solveeit Logo
Login

Question

Question: vander Waal's gas equation may be expressed as $Z=1+\frac{B}{V_m}+\frac{C}{V_m^2}+......$ where Vm=...

vander Waal's gas equation may be expressed as

Z=1+BVm+CVm2+......Z=1+\frac{B}{V_m}+\frac{C}{V_m^2}+...... where Vm= molar volume of gas. If B =-0.105Lmol−1^{-1} and C=400ml2^2 mol−2^{-2} at 127°C the value of vander Waal constant 'a' (in atm L2^2mol−2^{-2}) is (R = 0.08 L-atm/K-mol)

Answer

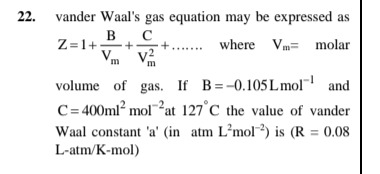
4

Explanation

Solution

The van der Waals equation for one mole of gas is:

(P+aVm2)(Vm−b)=RT(P + \frac{a}{V_m^2})(V_m - b) = RT

To express this in the virial form, we first rearrange it to solve for P:

P=RTVm−b−aVm2P = \frac{RT}{V_m - b} - \frac{a}{V_m^2}

Now, we introduce the compressibility factor Z:

Z=PVmRTZ = \frac{PV_m}{RT}

Substitute the expression for P into the equation for Z:

Z=VmRT(RTVm−b−aVm2)Z = \frac{V_m}{RT} \left( \frac{RT}{V_m - b} - \frac{a}{V_m^2} \right)

Z=VmVm−b−aVmRTVm2Z = \frac{V_m}{V_m - b} - \frac{aV_m}{RT V_m^2}

Z=11−b/Vm−aRTVmZ = \frac{1}{1 - b/V_m} - \frac{a}{RTV_m}

We use the binomial expansion for (1−x)−1=1+x+x2+x3+......(1-x)^{-1} = 1 + x + x^2 + x^3 + ...... where x=b/Vmx = b/V_m. Since VmV_m is typically large for gases, b/Vmb/V_m is a small quantity.

So, 11−b/Vm=1+bVm+b2Vm2+b3Vm3+......\frac{1}{1 - b/V_m} = 1 + \frac{b}{V_m} + \frac{b^2}{V_m^2} + \frac{b^3}{V_m^3} + ......

Substitute this back into the expression for Z:

Z=(1+bVm+b2Vm2+b3Vm3+......)−aRTVmZ = \left( 1 + \frac{b}{V_m} + \frac{b^2}{V_m^2} + \frac{b^3}{V_m^3} + ...... \right) - \frac{a}{RTV_m}

Group terms by powers of 1/Vm1/V_m:

Z=1+(b−aRT)1Vm+b2Vm2+b3Vm3+......Z = 1 + \left(b - \frac{a}{RT}\right)\frac{1}{V_m} + \frac{b^2}{V_m^2} + \frac{b^3}{V_m^3} + ......

This is the virial equation of state. Comparing it with the given form:

Z=1+BVm+CVm2+......Z=1+\frac{B}{V_m}+\frac{C}{V_m^2}+......

We can identify the second and third virial coefficients:

B=b−aRTB = b - \frac{a}{RT}

C=b2C = b^2

Given values:

B=−0.105 L mol−1B = -0.105 \text{ L mol}^{-1}

C=400 mL2 mol−2C = 400 \text{ mL}^2 \text{ mol}^{-2}

Temperature T=127∘C=127+273=400 KT = 127^\circ\text{C} = 127 + 273 = 400 \text{ K}

Gas constant R=0.08 L-atm/K-molR = 0.08 \text{ L-atm/K-mol}

First, convert the unit of C from mL2^2 to L2^2:

1 L=1000 mL1 \text{ L} = 1000 \text{ mL}

1 mL=10−3 L1 \text{ mL} = 10^{-3} \text{ L}

C=400 mL2 mol−2=400×(10−3 L)2 mol−2=400×10−6 L2 mol−2=0.0004 L2 mol−2C = 400 \text{ mL}^2 \text{ mol}^{-2} = 400 \times (10^{-3} \text{ L})^2 \text{ mol}^{-2} = 400 \times 10^{-6} \text{ L}^2 \text{ mol}^{-2} = 0.0004 \text{ L}^2 \text{ mol}^{-2}

Now, use the equation for C to find the van der Waals constant 'b':

b2=Cb^2 = C

b=C=0.0004 L2 mol−2b = \sqrt{C} = \sqrt{0.0004 \text{ L}^2 \text{ mol}^{-2}}

b=0.02 L mol−1b = 0.02 \text{ L mol}^{-1}

Next, use the equation for B to find the van der Waals constant 'a':

B=b−aRTB = b - \frac{a}{RT}

Rearrange to solve for 'a':

aRT=b−B\frac{a}{RT} = b - B

a=(b−B)RTa = (b - B)RT

Substitute the values of b, B, R, and T:

a=(0.02 L mol−1−(−0.105 L mol−1))×(0.08 L-atm/K-mol)×(400 K)a = (0.02 \text{ L mol}^{-1} - (-0.105 \text{ L mol}^{-1})) \times (0.08 \text{ L-atm/K-mol}) \times (400 \text{ K})

a=(0.02+0.105) L mol−1×(0.08×400) L-atm/mola = (0.02 + 0.105) \text{ L mol}^{-1} \times (0.08 \times 400) \text{ L-atm/mol}

a=(0.125) L mol−1×(32) L-atm/mola = (0.125) \text{ L mol}^{-1} \times (32) \text{ L-atm/mol}

a=18×32 atm L2 mol−2a = \frac{1}{8} \times 32 \text{ atm L}^2 \text{ mol}^{-2}

a=4 atm L2 mol−2a = 4 \text{ atm L}^2 \text{ mol}^{-2}

The value of van der Waals constant 'a' is 4 atm L2 mol−24 \text{ atm L}^2 \text{ mol}^{-2}.