Question

Let f be a twice differentiable function such that $f''(x)=-f(x)$, $g(x) = f'(x)$ and $h(x) = (f(x))^2 + (g(x))^2$. If h (5) = 1, then h (10) =

• A.
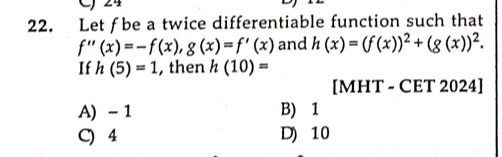
  • 1
• B. 1
• C. 4
• D. 10

Answer 1

Answer: (B)

1

Answer 2

Given the differential equation $f''(x) = -f(x)$ and $g(x) = f'(x)$. We are given $h(x) = (f(x))^2 + (g(x))^2$. To find $h(10)$, we first find the derivative of $h(x)$: $h'(x) = \frac{d}{dx}[(f(x))^2] + \frac{d}{dx}[(g(x))^2]$ Using the chain rule, this becomes: $h'(x) = 2f(x)f'(x) + 2g(x)g'(x)$

Substitute $g(x) = f'(x)$: $h'(x) = 2f(x)g(x) + 2g(x)g'(x)$

Now, find $g'(x)$: $g'(x) = \frac{d}{dx}[f'(x)] = f''(x)$

From the given condition, $f''(x) = -f(x)$. So, $g'(x) = -f(x)$

Substitute $g'(x) = -f(x)$ back into the expression for $h'(x)$: $h'(x) = 2f(x)g(x) + 2g(x)(-f(x))$ $h'(x) = 2f(x)g(x) - 2f(x)g(x)$ $h'(x) = 0$

Since the derivative of $h(x)$ is 0 for all $x$, $h(x)$ must be a constant function. Let $h(x) = C$, where $C$ is a constant.

We are given that $h(5) = 1$. Therefore, $C = 1$. So, $h(x) = 1$ for all values of $x$.

Consequently, $h(10) = 1$. The final answer is $\boxed{1}$ (Option B)