Question

In a vernier calliper, one main scale division is x cm and n division of vernier scale coincide with (n - 1) division of the main scale. The least count of the vernier calliper in cm is :-

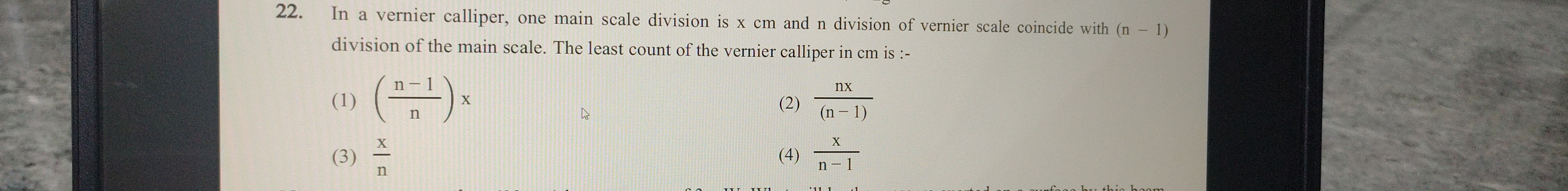
• A. $(\frac{n-1}{n})$x
• B. $\frac{nx}{(n-1)}$
• C. $\frac{x}{n}$
• D. $\frac{x}{n-1}$

Answer 1

Answer: (C)

$\frac{x}{n}$

Answer 2

The least count (LC) of a vernier calliper is defined as the difference between one main scale division (MSD) and one vernier scale division (VSD).

LC = 1 MSD - 1 VSD

Given:

1. One main scale division (MSD) = x cm.
2. n divisions of the vernier scale coincide with (n - 1) divisions of the main scale, which means: n VSD = (n - 1) MSD

From the second condition, we can express 1 VSD in terms of MSD:

1 VSD = $\frac{(n-1)}{n}$ MSD

Substitute this expression for 1 VSD into the least count formula:

LC = 1 MSD - $\frac{(n-1)}{n}$ MSD

LC = MSD $(1 - \frac{(n-1)}{n})$

LC = MSD $(\frac{n - (n-1)}{n})$

LC = MSD $(\frac{n - n + 1}{n})$

LC = MSD $(\frac{1}{n})$

Finally, substitute the value of 1 MSD = x cm:

LC = x $(\frac{1}{n})$ cm

LC = $\frac{x}{n}$ cm