Question
Question: If $A = \sin\frac{2\pi}{7} + \sin\frac{4\pi}{7} + \sin\frac{8\pi}{7}$ and $B = \cos\frac{2\pi}{7} + ...
If A=sin72π+sin74π+sin78π and B=cos72π+cos74π+cos78π then A2+B2 is equa
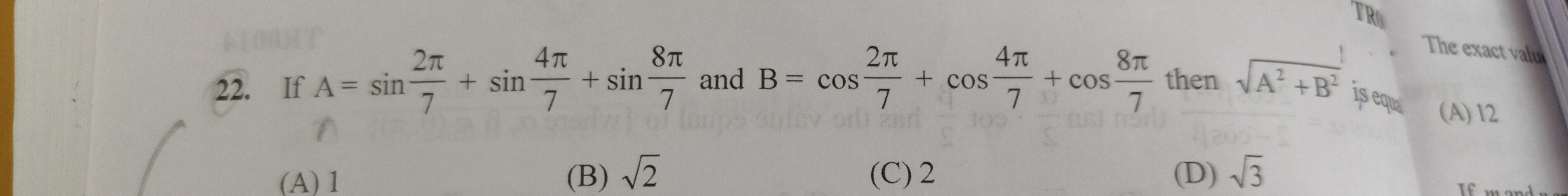
1
2
2
3
2
Solution
To find A2+B2, we can recognize this expression as the magnitude of a complex number. Let Z=B+iA. Substituting the given expressions for A and B: Z=(cos72π+cos74π+cos78π)+i(sin72π+sin74π+sin78π)
Group the terms using Euler's formula, eiθ=cosθ+isinθ: Z=(cos72π+isin72π)+(cos74π+isin74π)+(cos78π+isin78π) Z=ei72π+ei74π+ei78π
Let ω=ei72π. This is a primitive 7th root of unity. Then Z=ω1+ω2+ω4.
This sum is a Gaussian period for p=7. The quadratic residues modulo 7 are 12≡1, 22≡4, 32≡2. So the set of quadratic residues is R={1,2,4}. The sum Z=∑k∈Rωk is denoted as η0.
We know that for the 7th roots of unity, the sum of all roots is zero: 1+ω+ω2+ω3+ω4+ω5+ω6=0. Let η0=ω1+ω2+ω4 and η1=ω3+ω5+ω6. From the sum of all roots, we have 1+η0+η1=0, so η0+η1=−1.
Next, consider the product η0η1: η0η1=(ω1+ω2+ω4)(ω3+ω5+ω6) =ω1+3+ω1+5+ω1+6+ω2+3+ω2+5+ω2+6+ω4+3+ω4+5+ω4+6 =ω4+ω6+ω7+ω5+ω7+ω8+ω7+ω9+ω10 Since ω7=1, we can simplify the powers of ω: ω7=1, ω8=ω1, ω9=ω2, ω10=ω3. η0η1=ω4+ω6+1+ω5+1+ω1+1+ω2+ω3 Rearranging the terms: η0η1=3+(ω1+ω2+ω3+ω4+ω5+ω6) Since ∑k=16ωk=−1: η0η1=3+(−1)=2.
Now we have a system of equations for η0 and η1:
- η0+η1=−1
- η0η1=2 η0 and η1 are the roots of the quadratic equation x2−(η0+η1)x+η0η1=0: x2−(−1)x+2=0⟹x2+x+2=0. Using the quadratic formula, x=2a−b±b2−4ac: x=2(1)−1±12−4(1)(2)=2−1±1−8=2−1±−7=2−1±i7.
So, {η0,η1}={2−1+i7,2−1−i7}. To determine which value corresponds to η0=Z=B+iA, we need to check the sign of its imaginary part A. A=sin72π+sin74π+sin78π. Note that sin78π=sin(π+7π)=−sin7π. So, A=sin72π+sin74π−sin7π. Also, sin74π=sin(π−74π)=sin73π. A=sin72π+sin73π−sin7π. Let x=7π. Then A=sin(2x)+sin(3x)−sin(x). A=2sinxcosx+(3sinx−4sin3x)−sinx A=sinx(2cosx+3−4sin2x−1) A=sinx(2cosx+2−4(1−cos2x)) A=sinx(2cosx+2−4+4cos2x) A=sinx(4cos2x+2cosx−2) A=2sinx(2cos2x+cosx−1) A=2sinx(2cosx−1)(cosx+1). For x=7π, x∈(0,2π), so sinx>0 and cosx>0. Also, cosx+1>0. Since 7π<3π, and cosx is a decreasing function in (0,π), we have cos(7π)>cos(3π)=21. Therefore, 2cos(7π)>1, which means 2cos(7π)−1>0. Thus, A>0.
Since A is the imaginary part of Z=η0, and A>0, we must choose the root with the positive imaginary part: Z=η0=2−1+i7. So, B=Re(Z)=−21 and A=Im(Z)=27.
The problem asks for A2+B2, which is the magnitude of the complex number Z. A2+B2=∣Z∣=2−1+i7 ∣Z∣=21(−1)2+(7)2 ∣Z∣=211+7 ∣Z∣=218 ∣Z∣=21(22) ∣Z∣=2.
