Question
Question: If a, b, c are real then the value of determinant $\begin{array}{ccc}a^{2}+1 & a b & a c \\ a b & b^...
If a, b, c are real then the value of determinant a2+1abacabb2+1bcacbcc2+1 = 1 if
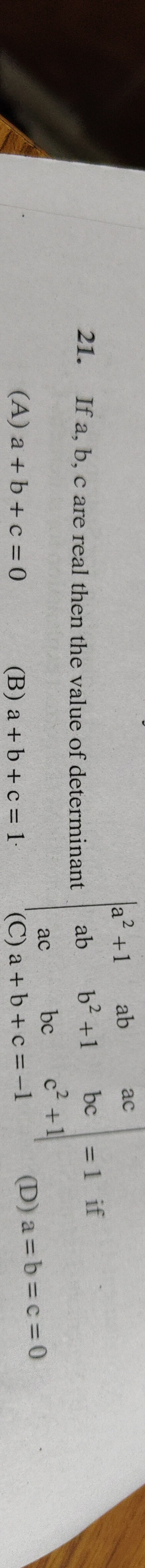
a+b+c=0
a+b+c=1
a+b+c=-1
a=b=c=0
a=b=c=0
Solution
To find the value of the determinant and the condition for it to be 1, we can use properties of determinants.
The given determinant is: D=a2+1abacabb2+1bcacbcc2+1
Step 1: Transform the determinant
Multiply C1 by a, C2 by b, C3 by c. To keep the determinant value unchanged, we must divide the entire determinant by abc.
D=abc1a(a2+1)a(ab)a(ac)b(ab)b(b2+1)b(bc)c(ac)c(bc)c(c2+1)
D=abc1a3+aa2ba2cab2b3+bb2cac2bc2c3+c
Now, take a common from R1, b common from R2, and c common from R3.
D=abcabca2+1a2a2b2b2+1b2c2c2c2+1
D=a2+1a2a2b2b2+1b2c2c2c2+1
Step 2: Simplify the transformed determinant
Let x=a2, y=b2, z=c2. The determinant becomes:
D=x+1xxyy+1yzzz+1
Apply the column operation C1→C1+C2+C3:
D=x+y+z+1x+y+z+1x+y+z+1yy+1yzzz+1
Take (x+y+z+1) common from C1:
D=(x+y+z+1)111yy+1yzzz+1
Apply row operations R2→R2−R1 and R3→R3−R1:
D=(x+y+z+1)100y10z01
Expand the determinant along C1:
D=(x+y+z+1)⋅1⋅(1⋅1−0⋅0)
D=(x+y+z+1)⋅1
D=x+y+z+1
Step 3: Substitute back x,y,z and find the condition
Substitute x=a2,y=b2,z=c2 back into the expression for D:
D=a2+b2+c2+1
The problem states that the value of the determinant is 1.
So, a2+b2+c2+1=1
a2+b2+c2=0
Since a,b,c are real numbers, their squares (a2,b2,c2) are non-negative. The sum of non-negative terms can be zero if and only if each term is zero.
Therefore, a2=0, b2=0, and c2=0.
This implies a=0, b=0, and c=0.
The condition for the determinant to be 1 is a=b=c=0.
