Question

$\frac{1}{log_{\sqrt{bc}} abc}+\frac{1}{log_{\sqrt{ca}} abc}+\frac{1}{log_{\sqrt{ab}} abc}$ has the value equal to-

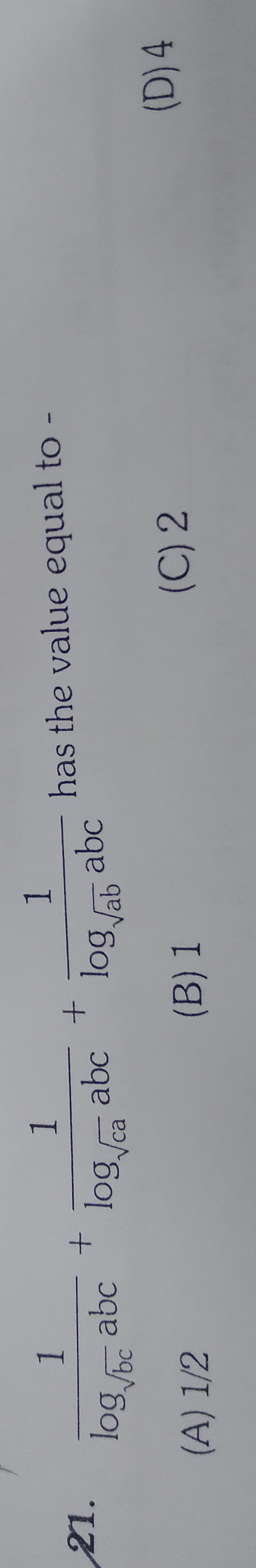
• A. 1/2
• B. 1
• C. 2
• D. 4

Answer 1

Answer: (B)

1

Answer 2

Let the given expression be $E$. $E = \frac{1}{log_{\sqrt{bc}} abc}+\frac{1}{log_{\sqrt{ca}} abc}+\frac{1}{log_{\sqrt{ab}} abc}$ Using the property $\frac{1}{log_x y} = log_y x$: $E = log_{abc} \sqrt{bc} + log_{abc} \sqrt{ca} + log_{abc} \sqrt{ab}$ Using the property $log_b x + log_b y + log_b z = log_b (xyz)$: $E = log_{abc} (\sqrt{bc} \times \sqrt{ca} \times \sqrt{ab})$ Simplify the argument: $\sqrt{bc} \times \sqrt{ca} \times \sqrt{ab} = (bc)^{1/2} (ca)^{1/2} (ab)^{1/2} = a^{1/2}b^{1/2} b^{1/2}c^{1/2} c^{1/2}a^{1/2} = a^1 b^1 c^1 = abc$ So, $E = log_{abc} (abc)$ Using the property $log_b b = 1$: $E = 1$