Question

Given the equation $2^{1 + |\cos x| + |\cos x|^2 + \dots} \;=\; 4,$ show that this implies $2^{\frac{1}{1 - |\cos x|}} \;=\; 2^2$ and hence find all solutions for $x$.

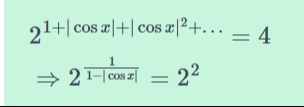
Answer 1

$\boxed{|\cos x| = \tfrac12 \;\Longrightarrow\;\cos x = \pm\tfrac12,\quad x = \pm\tfrac{\pi}{3} + 2\pi n\;\text{or}\;x = \pm\tfrac{2\pi}{3} + 2\pi n,\;n\in\mathbb{Z}.}$

Answer 2

Step 1: Sum the infinite series

We recognize

$$1 + |\cos x| + |\cos x|^2 + \dots$$

as a geometric series with first term $1$ and ratio $r = |\cos x|$. For convergence we need $|\cos x|<1$. The sum is

$$\frac{1}{1 - |\cos x|}.$$

Step 2: Equate to the given power

The equation becomes

$$2^{\frac{1}{1 - |\cos x|}} = 4 = 2^2.$$

Hence,

$$\frac{1}{1 - |\cos x|} = 2 \quad\Longrightarrow\quad 1 - |\cos x| = \tfrac12 \quad\Longrightarrow\quad |\cos x| = \tfrac12.$$

Step 3: Solve for $x$

Since $|\cos x| = \tfrac12$, we have

$$\cos x = \pm \tfrac12.$$

The general solutions on the real line are

$$x = \pm \frac{\pi}{3} + 2\pi n \quad\text{or}\quad x = \pm \frac{2\pi}{3} + 2\pi n, \quad n\in\mathbb{Z}.$$