Question
Question: Two light strings, each of length $l$, are fixed at points A and B on a fixed horizontal rod xy. A s...
Two light strings, each of length l, are fixed at points A and B on a fixed horizontal rod xy. A small bob is tied by both strings and in equilibrium, the strings are making angle 45∘ with the rod. If the bob is slightly displaced normal to the plane of the strings and released then period of the resulting small oscillation will be:
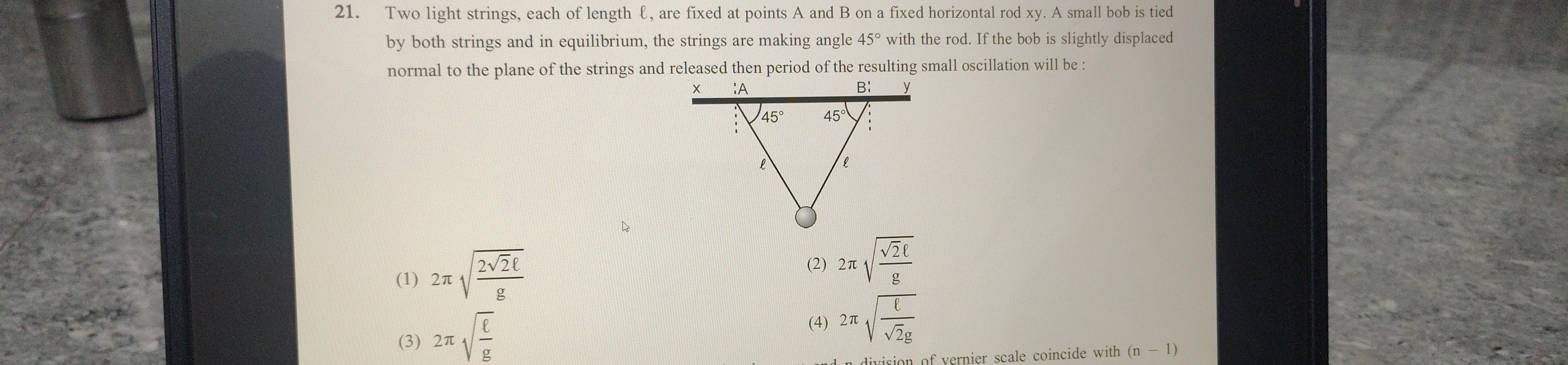
2πg22l
2πg2l
2πgl
2π2gl
2\pi \sqrt{\frac{l}{\sqrt{2}g}}
Solution
The problem describes a bob tied by two light strings of length l each, fixed at points A and B on a horizontal rod. In equilibrium, the strings make an angle of 45∘ with the rod. The bob is then slightly displaced normal to the plane of the strings and released. We need to find the period of the resulting small oscillation.
-
Equilibrium Analysis: In equilibrium, the bob is at a depth h=lsin45∘=l/2 below the rod. The horizontal distance from the center of the rod to each string's attachment point is d=lcos45∘=l/2. The vertical components of tension balance the weight: 2Tcos45∘=mg, so T=2mg2.
-
Displacement and Restoring Force: When the bob is displaced by a small distance z normal to the plane of the strings (along the z-axis), its new position is (0,y,z). Since the strings are inextensible, the distance from each fixed point (e.g., A at (−d,0,0)) to the bob must be l.
So, (−d−0)2+(0−y)2+(0−z)2=l2 d2+y2+z2=l2 (l/2)2+y2+z2=l2 l2/2+y2+z2=l2⟹y2+z2=l2/2.
For small z, the vertical position y=−l2/2−z2≈−(l/2)(1−z2/l2).
The forces acting on the bob are its weight mg downwards and the tension T in each string. Due to symmetry, the tension in both strings is equal.
The restoring force in the z-direction is Fz=−2Tsinθz, where θz is the angle the string makes with the y-z plane. More precisely, it's the component of tension in the z-direction.
The z-component of force from each string is Tl−z.
So, the net restoring force is Fz=−2Tlz.
In the y-direction, for small oscillations, the bob is nearly in equilibrium, so 2Tl−y−mg=0⟹T=2∣y∣mgl.
Substitute ∣y∣=l2/2−z2: T=2l2/2−z2mgl.
Now substitute T into the expression for Fz: Fz=−2(2l2/2−z2mgl)lz=−l2/2−z2mgz.
For small oscillations, z≪l/2, so l2/2−z2≈l2/2=l/2.
Thus, Fz≈−l/2mgz=−lmg2z.
-
Period of Oscillation: The equation of motion is mdt2d2z=−(lmg2)z.
This is a simple harmonic motion equation mdt2d2z=−kz, where k=lmg2.
The angular frequency is ω=mk=mmg2/l=lg2.
The period of oscillation is P=ω2π=2πg2l.
This can be rationalized as P=2πg22l2=2π2g2l.
Comparing with the given options, 2π2gl matches option (4).
