Question

Two adjacent sides of a rhombus are 2x + 3y = a - 5 and 3x + 2y = 4-2a and its diagonals intersect at the point (1,2), then a can be -

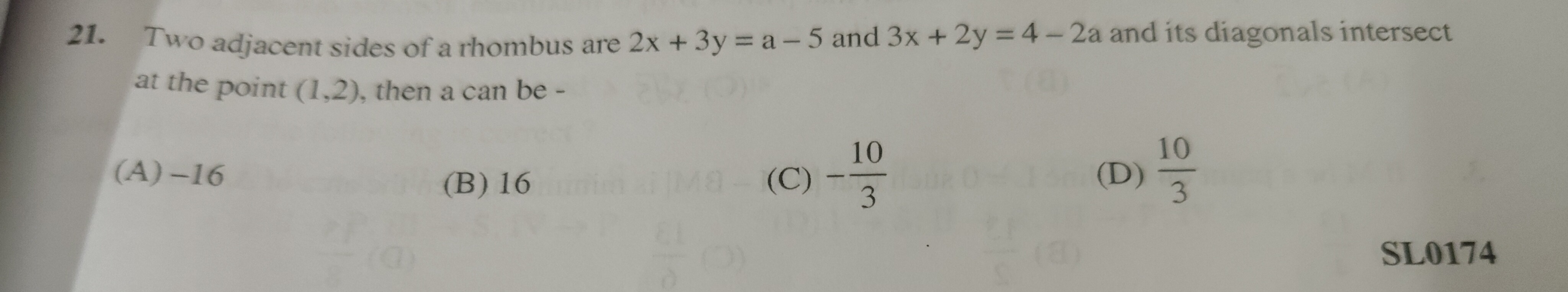
• A. -16
• B. 16
• C. -$\frac{10}{3}$
• D. $\frac{10}{3}$

Answer 1

Answer: (A), (D)

Both -16 and $\frac{10}{3}$ are correct.

Answer 2

A rhombus has diagonals that bisect each other at right angles. The intersection point of the diagonals is the center of the rhombus. The distance from the center to each side must be equal.

The equations of the adjacent sides are: $L_1: 2x + 3y - (a - 5) = 0$ $L_2: 3x + 2y - (4 - 2a) = 0$

The center of the rhombus is $(1, 2)$. The distance from a point $(x_0, y_0)$ to a line $Ax + By + C = 0$ is given by $d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$.

Distance from $(1, 2)$ to $L_1$: $d_1 = \frac{|2(1) + 3(2) - (a - 5)|}{\sqrt{2^2 + 3^2}} = \frac{|2 + 6 - a + 5|}{\sqrt{4 + 9}} = \frac{|13 - a|}{\sqrt{13}}$

Distance from $(1, 2)$ to $L_2$: $d_2 = \frac{|3(1) + 2(2) - (4 - 2a)|}{\sqrt{3^2 + 2^2}} = \frac{|3 + 4 - 4 + 2a|}{\sqrt{9 + 4}} = \frac{|3 + 2a|}{\sqrt{13}}$

Since $d_1 = d_2$: $\frac{|13 - a|}{\sqrt{13}} = \frac{|3 + 2a|}{\sqrt{13}}$ $|13 - a| = |3 + 2a|$

This equality holds if: Case 1: $13 - a = 3 + 2a$ $10 = 3a$ $a = \frac{10}{3}$

Case 2: $13 - a = -(3 + 2a)$ $13 - a = -3 - 2a$ $16 = -a$ $a = -16$

Therefore, the possible values for 'a' are $\frac{10}{3}$ and $-16$.