Question
Question: The three vectors $\vec{a}$, $\vec{b}$ and $\vec{c}$ be such that $\vec{c}$ is coplanar with $\vec{a...
The three vectors a, b and c be such that c is coplanar with a and b, a⋅c=7 and b is perpendicular to c, where a=−i^+j^+k^ and b=2i^+k^, then the value of 2∣a+b+c∣2 is _____.
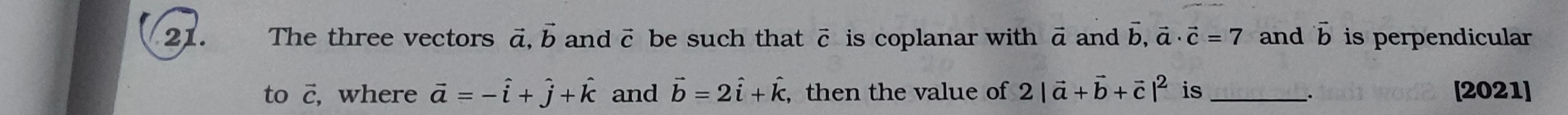
75
150
37.5
60
75
Solution
-
Coplanarity and Perpendicularity: Since c is coplanar with a and b, we can write c=xa+yb for some scalars x and y. Given b⋅c=0, we substitute c: b⋅(xa+yb)=0 x(b⋅a)+y(b⋅b)=0 Calculate dot products: a=−i^+j^+k^, b=2i^+k^ b⋅a=(2)(−1)+(0)(1)+(1)(1)=−1 b⋅b=∣b∣2=22+02+12=5 Substituting these: x(−1)+y(5)=0⟹−x+5y=0⟹x=5y. So, c=5ya+yb=y(5a+b).
-
Using a⋅c=7: Substitute c=y(5a+b) into a⋅c=7: a⋅[y(5a+b)]=7 y[5(a⋅a)+(a⋅b)]=7 Calculate required dot products: a⋅a=∣a∣2=(−1)2+12+12=3 a⋅b=−1 (calculated earlier) Substituting these: y[5(3)+(−1)]=7⟹y(15−1)=7⟹14y=7⟹y=21. Thus, c=21(5a+b).
-
Calculating a+b+c: a+b+c=a+b+21(5a+b) =(1+25)a+(1+21)b =27a+23b
-
Calculating ∣a+b+c∣2: Let S=27a+23b. ∣S∣2=(27a+23b)⋅(27a+23b) =(27)2∣a∣2+(23)2∣b∣2+2(27)(23)(a⋅b) Using ∣a∣2=3, ∣b∣2=5, a⋅b=−1: ∣S∣2=449(3)+49(5)+2(421)(−1) ∣S∣2=4147+445−442=4147+45−42=4150=275.
-
Final Value: The question asks for 2∣a+b+c∣2. 2×∣S∣2=2×275=75.
