Question

The equation of the tangent to the curve $y=4xe^x$ at $\displaystyle\bigl(-1,\,-\tfrac{4}{e}\bigr)$ is

• A. $x = -1$
• B. $x - \tfrac{e}{4}y = 0$
• C. $y = -\tfrac{4}{e}$
• D. $6x - \tfrac{e}{4}y = -5$

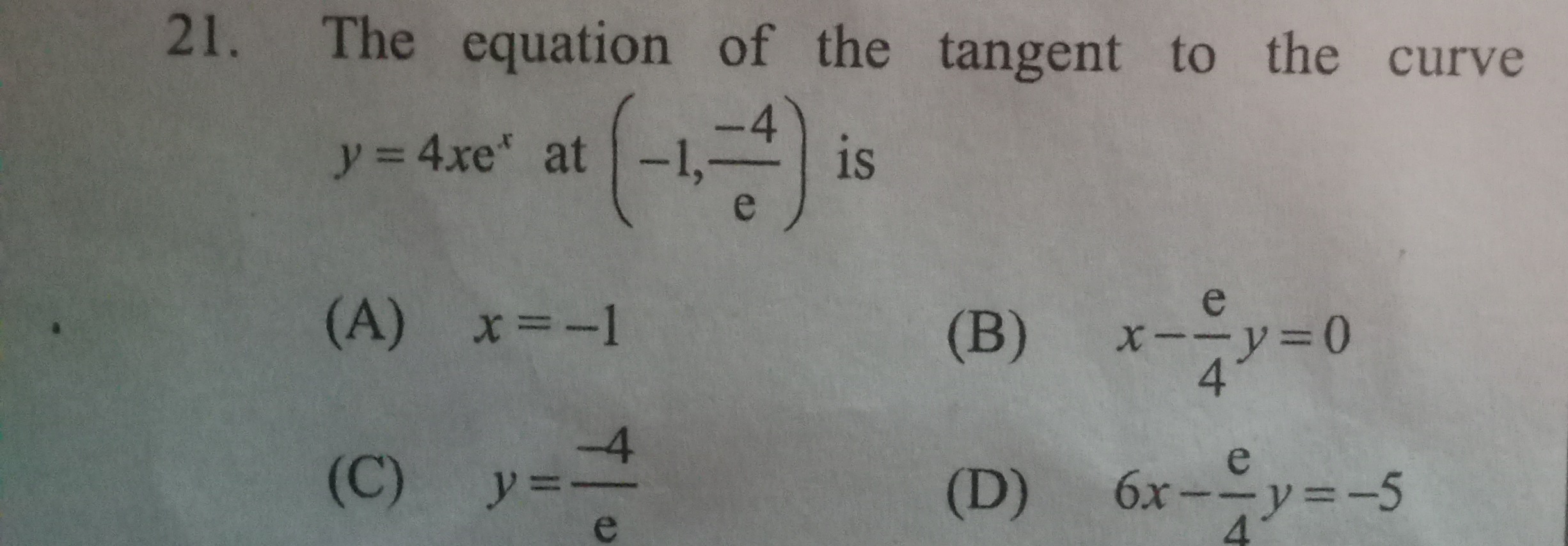
Answer 1

Answer: (C)

y = -\tfrac{4}{e}

Answer 2

1. Compute the derivative:

$$y = 4x e^x \quad\Longrightarrow\quad \frac{dy}{dx} =4e^x +4x e^x =4e^x(1+x).$$

2. At $x=-1$:

$$y'\bigl(-1\bigr) =4e^{-1}(1-1)=0,$$

so the tangent is horizontal.
3. The point is $\bigl(-1,-\tfrac{4}{e}\bigr)$, so the equation is

$$y = -\frac{4}{e}.$$