Question
Question: Let $f(x) = 3x^{10}-7x^8+5x^6-21x^3+3x^2-7$ $265 \left( \lim\limits_{h \to 0} \frac{h^4+3h^2}{(f(1-...
Let f(x)=3x10−7x8+5x6−21x3+3x2−7
265(h→0lim(f(1−h)−f(1))sin5hh4+3h2)=
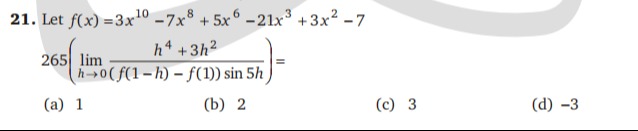
1
2
3
-3
3
Solution
The given expression is 265(h→0lim(f(1−h)−f(1))sin5hh4+3h2). Let's evaluate the limit part: L=h→0lim(f(1−h)−f(1))sin5hh4+3h2.
As h→0, the numerator h4+3h2→04+3(0)2=0. As h→0, 1−h→1, so f(1−h)→f(1). Thus, the term f(1−h)−f(1)→0. Also, as h→0, sin5h→sin(0)=0. The limit is of the indeterminate form 00.
We can rewrite the expression to use the definition of the derivative f′(a)=x→alimx−af(x)−f(a). Let's consider the term f(1−h)−f(1). Let x=1−h. As h→0, x→1. Then f(1−h)−f(1)=f(x)−f(1). The denominator difference is (1−h)−1=−h. So, h→0lim−hf(1−h)−f(1)=x→1limx−1f(x)−f(1)=f′(1). Therefore, for small h, f(1−h)−f(1)≈−hf′(1).
We also use the standard limit x→0limxsinx=1. For small h, sin5h≈5h.
Let's rewrite the limit expression by dividing the numerator and denominator by appropriate powers of h: L=h→0lim(f(1−h)−f(1))sin5hh2(h2+3) L=h→0lim(−hf(1−h)−f(1))(−h)(5hsin5h)(5h)h2(h2+3) L=h→0lim(−5h2)(−hf(1−h)−f(1))(5hsin5h)h2(h2+3) For h=0, we can cancel h2 from the numerator and denominator: L=h→0lim−5(−hf(1−h)−f(1))(5hsin5h)h2+3
Now, we evaluate the limit of each part as h→0: h→0lim(h2+3)=02+3=3. h→0lim−hf(1−h)−f(1)=f′(1) by the definition of the derivative. h→0lim5hsin5h=1 by the standard limit.
So, the limit L is: L=−5⋅f′(1)⋅13=−5f′(1)3.
Now we need to find f′(1). f(x)=3x10−7x8+5x6−21x3+3x2−7 The derivative f′(x) is: f′(x)=dxd(3x10)−dxd(7x8)+dxd(5x6)−dxd(21x3)+dxd(3x2)−dxd(7) f′(x)=3(10x9)−7(8x7)+5(6x5)−21(3x2)+3(2x)−0 f′(x)=30x9−56x7+30x5−63x2+6x.
Now, evaluate f′(1): f′(1)=30(1)9−56(1)7+30(1)5−63(1)2+6(1) f′(1)=30−56+30−63+6 f′(1)=(30+30+6)−(56+63) f′(1)=66−119 f′(1)=−53.
Substitute the value of f′(1) into the limit expression: L=−5(−53)3=2653.
The question asks for the value of 265×L. 265×L=265×2653=3.
The final answer is 3.
