Question
Question: If the value of $\lim_{x\to0}(2-\cos x\sqrt{\cos 2x})^{(\frac{x+2}{x^2})}$ is equal to $e^a$, then a...
If the value of limx→0(2−cosxcos2x)(x2x+2) is equal to ea, then a is equal to
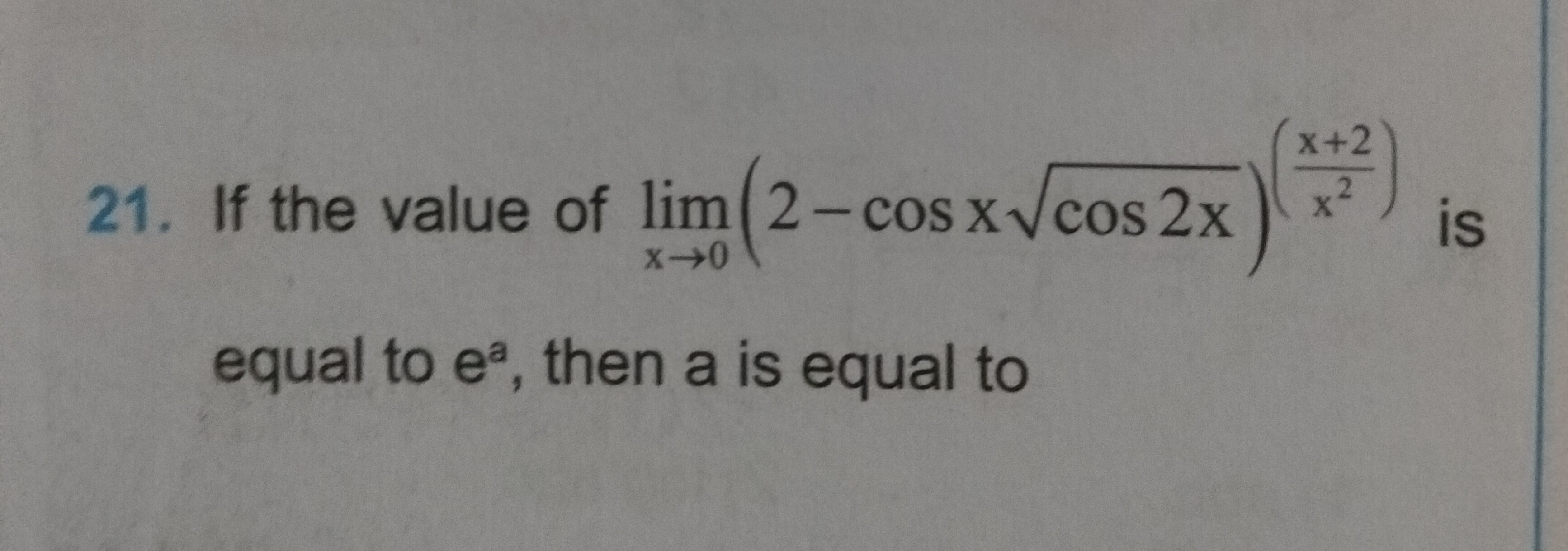
3
Solution
The given limit is of the form limx→0(2−cosxcos2x)(x2x+2).
Let f(x)=2−cosxcos2x and g(x)=x2x+2.
As x→0: f(x)→2−cos(0)cos(0)=2−1⋅1=2−1=1. g(x)→020+2=02→∞.
This is an indeterminate form of type 1∞. For limits of the form limx→a[f(x)]g(x) which are 1∞, we use the formula: L=elimx→ag(x)[f(x)−1] In this case, f(x)−1=(2−cosxcos2x)−1=1−cosxcos2x. So, the exponent is A=limx→0x2x+2(1−cosxcos2x). We can write this as: A=(limx→0(x+2))⋅(limx→0x21−cosxcos2x) The first limit is 0+2=2. Let's evaluate the second limit, H=limx→0x21−cosxcos2x. As x→0, the numerator 1−cos(0)cos(0)=1−1=0, and the denominator 02=0. So, it is a 00 indeterminate form, and we can apply L'Hopital's Rule.
Let N(x)=1−cosxcos2x. Let D(x)=x2.
Differentiating N(x): N′(x)=−((−sinx)cos2x+cosx⋅2cos2x1⋅(−sin2x⋅2)) N′(x)=sinxcos2x+cos2xcosxsin2x Using sin2x=2sinxcosx: N′(x)=sinxcos2x+cos2xcosx(2sinxcosx) N′(x)=sinx(cos2x+cos2x2cos2x) N′(x)=sinx(cos2xcos2x+2cos2x) Using the identity cos2x=2cos2x−1, we have cos2x+2cos2x=(2cos2x−1)+2cos2x=4cos2x−1. So, N′(x)=sinxcos2x4cos2x−1.
Differentiating D(x): D′(x)=2x.
Now, apply L'Hopital's Rule: H=limx→0D′(x)N′(x)=limx→02xsinxcos2x4cos2x−1 H=limx→0(xsinx)⋅21⋅(cos2x4cos2x−1) We know that limx→0xsinx=1. Substitute x=0 into the remaining terms: H=1⋅21⋅cos(0)4cos2(0)−1 H=21⋅14(1)2−1=21⋅14−1=21⋅3=23 Now, substitute this value of H back into the expression for A: A=2⋅H=2⋅23=3 Therefore, the original limit L=eA=e3. Given that L=ea, we have ea=e3. Thus, a=3.
