Question

If a, b, c, d be positive real number such that $a+b+c+d = \frac{4}{3}$, then the minimum value of $\sqrt{\frac{1}{b+c+d}} + \sqrt{\frac{1}{c+d+a}} + \sqrt{\frac{1}{d+a+b}} + \sqrt{\frac{1}{a+b+c}}$ is equal to _________.

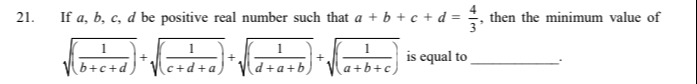
Answer 1

4

Answer 2

Let $S = a+b+c+d = \frac{4}{3}$. The given expression is

$$E = \sqrt{\frac{1}{b+c+d}} + \sqrt{\frac{1}{c+d+a}} + \sqrt{\frac{1}{d+a+b}} + \sqrt{\frac{1}{a+b+c}}.$$

Notice that each denominator can be written as $S - x$ where $x$ is one of $a, b, c, d$. Thus, the expression becomes:

$$E = \sqrt{\frac{1}{S - a}} + \sqrt{\frac{1}{S - b}} + \sqrt{\frac{1}{S - c}} + \sqrt{\frac{1}{S - d}}.$$

Since the problem is symmetric in $a, b, c, d$ and each term involves $(S-x)^{-1/2}$ which is a convex function in $x$ (as $\frac{d^2}{dx^2} (S-x)^{-1/2} > 0$), by the symmetry and convexity, the minimum occurs when

$$a = b = c = d = \frac{S}{4} = \frac{\frac{4}{3}}{4} = \frac{1}{3}.$$

Substitute $a = b = c = d = \frac{1}{3}$ in any term:

$$S - a = \frac{4}{3} - \frac{1}{3} = 1.$$

Thus, each term becomes:

$$\sqrt{\frac{1}{1}} = 1.$$

So,

$$E = 4 \times 1 = 4.$$