Question

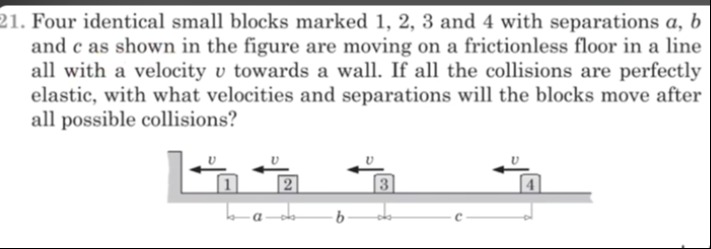
Four identical small blocks marked 1, 2, 3 and 4 with separations a, b and c as shown in the figure are moving on a frictionless floor in a line all with a velocity $v$ towards a wall. If all the collisions are perfectly elastic, with what velocities and separations will the blocks move after all possible collisions?

Answer 1

Velocities: Block 1: -v, Block 2: -v, Block 3: -v, Block 4: +v. Separations: 1-2: a, 2-3: b

Answer 2

The problem describes four identical blocks moving towards a wall on a frictionless floor. All blocks initially have the same velocity $v$ towards the wall. The collisions are perfectly elastic. We need to determine the velocities and separations of the blocks after all possible collisions.

Let the wall be at $x=0$ and the blocks are moving in the negative x direction. The initial velocity of all blocks is $-v$. Since the blocks are identical and the collisions are perfectly elastic, when two blocks collide, they exchange velocities. When a block collides with the wall (which can be considered as a very massive object), it rebounds with the same speed in the opposite direction.

The blocks are arranged in a line with separations $a$, $b$, and $c$. Block 1 is closest to the wall, followed by 2, 3, and 4. The sequence of events is as follows:

1. Block 1 collides with the wall. Since the collision is perfectly elastic, block 1 rebounds with velocity $+v$. The wall remains stationary.

2. After the collision with the wall, block 1 has velocity $+v$, while blocks 2, 3, and 4 still have velocity $-v$. Since block 1 is moving to the right and block 2 is moving to the left, they will collide. This is a collision between two identical blocks moving towards each other with speeds $v$. In a perfectly elastic collision between identical masses, the velocities are exchanged. So, block 1 will get the velocity of block 2, and block 2 will get the velocity of block 1. The velocity of block 1 becomes $-v$, and the velocity of block 2 becomes $+v$.

3. Now, block 2 has velocity $+v$, and block 3 has velocity $-v$. They will collide. Similar to the previous collision, they will exchange velocities. The velocity of block 2 becomes $-v$, and the velocity of block 3 becomes $+v$.

4. Now, block 3 has velocity $+v$, and block 4 has velocity $-v$. They will collide. They will exchange velocities. The velocity of block 3 becomes $-v$, and the velocity of block 4 becomes $+v$.

After these collisions, the velocities of the blocks are:

• Velocity of block 1: $-v$
• Velocity of block 2: $-v$
• Velocity of block 3: $-v$
• Velocity of block 4: $+v$

Blocks 1, 2, and 3 are moving to the left with velocity $-v$. Since they are moving in the same direction with the same velocity, the separations between them will remain constant. The separation between block 1 and block 2 will be $a$, and the separation between block 2 and block 3 will be $b$. Block 4 is moving to the right with velocity $+v$. Since block 4 is moving away from blocks 1, 2, and 3, there will be no further collisions between block 4 and the other blocks. The separation between block 3 and block 4 will increase over time.

The question asks for the velocities and separations after all possible collisions. All collisions between the blocks have occurred as described above. Since blocks 1, 2, and 3 are moving together, and block 4 is moving away, there will be no further collisions.

The final velocities are: $v_1 = -v$ $v_2 = -v$ $v_3 = -v$ $v_4 = +v$

The separations between blocks 1 and 2, and blocks 2 and 3 remain the same as their initial separations, $a$ and $b$, respectively, because they are moving with the same velocity. The separation between block 3 and block 4 will be increasing. The question asks for the separations after all possible collisions, which implies the state when no more collisions will occur. In this state, blocks 1, 2, and 3 are moving together, and block 4 is moving away. Thus, the separations between 1-2 and 2-3 are $a$ and $b$. The separation between 3 and 4 will be increasing. However, the question asks for "separations", which usually refers to the distances between adjacent blocks.

The final velocities are $v_1 = -v, v_2 = -v, v_3 = -v, v_4 = +v$. The final separations are:

• Separation between 1 and 2: $a$
• Separation between 2 and 3: $b$
• Separation between 3 and 4: increasing from $c$.

Assuming the question is asking for the constant separations between the blocks that move together and the velocity of the block moving in the opposite direction, the answer is as described above. If the question asks for the separations at a specific time after all collisions, that time is not specified. Given the context of such problems, it is likely asking for the constant separations between groups of blocks moving together and the velocities of the blocks.

Final velocities: $v_1 = -v, v_2 = -v, v_3 = -v, v_4 = +v$. Final separations: Separation between 1 and 2 is $a$, separation between 2 and 3 is $b$. The separation between 3 and 4 is increasing.

Since it's a multiple choice question and no options are provided, we assume the question is asking for the final velocities and the constant separations between the blocks that maintain constant separation.

Final Answer is the set of final velocities and the constant separations. Velocities: Block 1: $-v$, Block 2: $-v$, Block 3: $-v$, Block 4: $+v$. Separations: Separation between 1 and 2 is $a$, separation between 2 and 3 is $b$.