Question

Evaluate: $\left\{\left(\frac{1}{\sqrt{27}}\right)^{2-\left[\left(\log_5 13\right)/\left(2\log_5 9\right)\right]}\right\}^{1/2}$

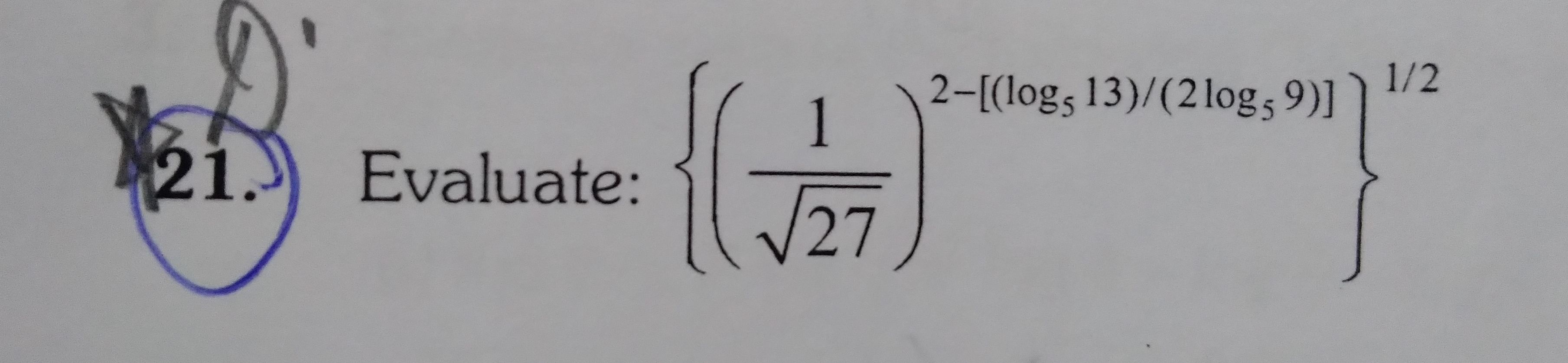
Answer 1

The evaluated expression is $3^{-3/2} \times 13^{3/16}$.

Answer 2

1. Simplify the base: $\frac{1}{\sqrt{27}} = 3^{-3/2}$.
2. Simplify the exponent term $\frac{\log_5 13}{2\log_5 9}$:
   • $2\log_5 9 = \log_5 9^2 = \log_5 81$.
   • $\frac{\log_5 13}{\log_5 81} = \log_{81} 13$ (using change of base).
3. The exponent of the base is $2 - \log_{81} 13$.
4. The expression becomes $\left\{(3^{-3/2})^{2 - \log_{81} 13}\right\}^{1/2}$.
5. Apply exponent rules: $(a^m)^n = a^{mn}$:
   • $3^{(-3/2) \times \frac{1}{2} \times (2 - \log_{81} 13)} = 3^{-\frac{3}{4}(2 - \log_{81} 13)}$.
6. Expand the exponent: $3^{-\frac{3}{2} + \frac{3}{4}\log_{81} 13} = 3^{-3/2} \times 3^{\frac{3}{4}\log_{81} 13}$.
7. Simplify $3^{\frac{3}{4}\log_{81} 13}$:
   • $\frac{3}{4}\log_{81} 13 = \frac{3}{4} \times \frac{\log_3 13}{\log_3 81} = \frac{3}{4} \times \frac{\log_3 13}{4} = \frac{3}{16}\log_3 13$.
   • $3^{\frac{3}{16}\log_3 13} = 3^{\log_3 13^{3/16}} = 13^{3/16}$.
8. The final evaluated form is $3^{-3/2} \times 13^{3/16}$.