Question

A solid sphere having uniform charge density and radius R is shown in figure. A spherical cavity of radius $\frac{R}{2}$ is hollowed out. What is potential of O? (Assuming potential at infinity to be zero)

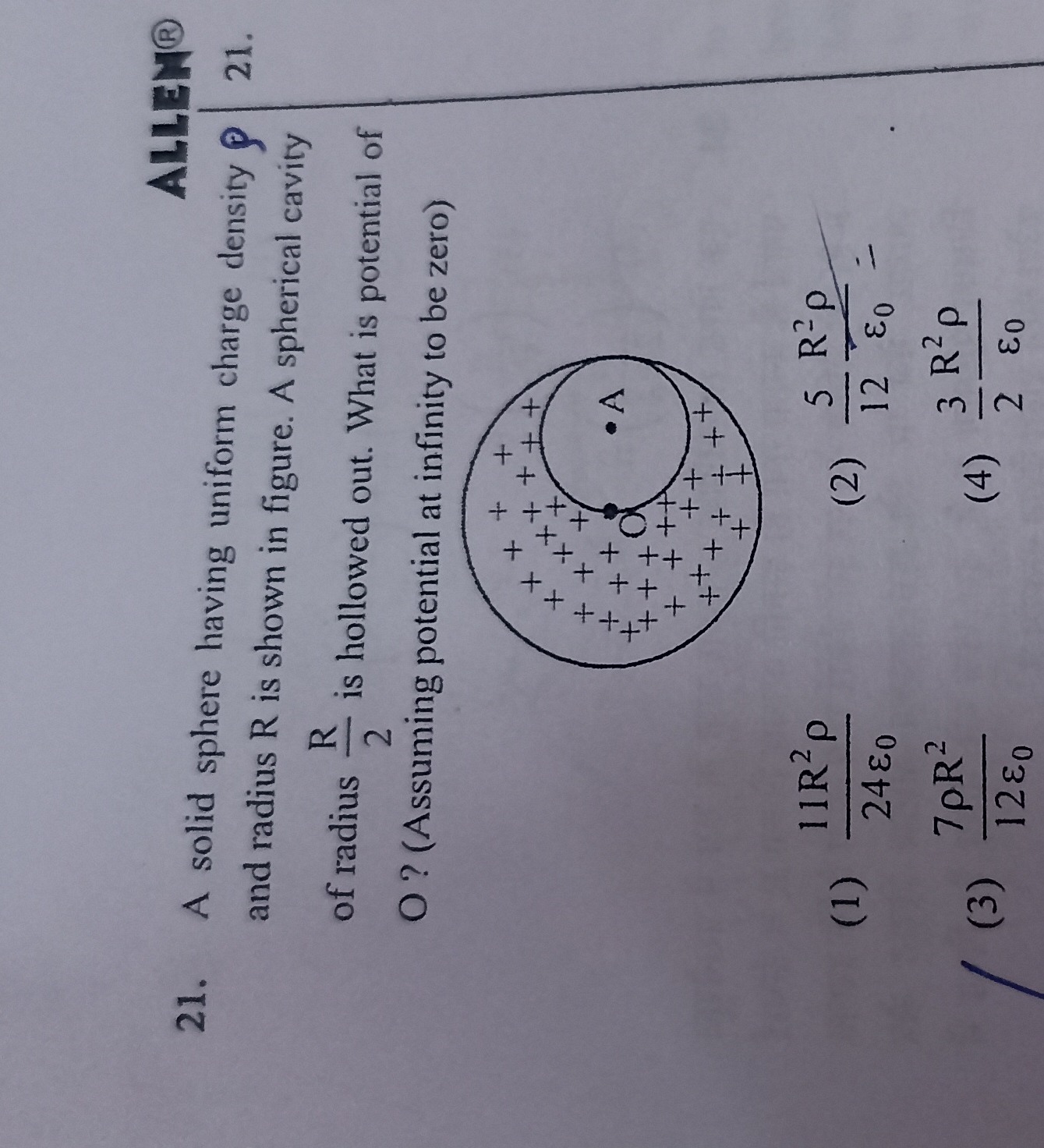
• A. $\frac{11R^2\rho}{24\epsilon_0}$
• B. $\frac{5R^2\rho}{12\epsilon_0}$
• C. $\frac{7\rho R^2}{12\epsilon_0}$
• D. $\frac{3R^2\rho}{2\epsilon_0}$

Answer 1

Answer: (B)

$\frac{5R^2\rho}{12\epsilon_0}$

Answer 2

The problem is solved using the principle of superposition.

1. Consider a complete solid sphere of radius R with uniform charge density $\rho$. Its center is C.
2. Consider a smaller solid sphere of radius R/2 with uniform charge density $-\rho$. Its center is A. This sphere effectively creates the cavity.
3. From the figure, the cavity is shifted such that its rightmost point touches the surface of the large sphere. If the center of the large sphere C is at the origin, the center of the cavity A is at a distance $d = R - R/2 = R/2$ from C.
4. Point O is marked as the leftmost point of the cavity. Given A is at $(R/2, 0, 0)$ and the cavity radius is $R/2$, O must be at $(R/2 - R/2, 0, 0) = (0,0,0)$. So, O is the center of the large sphere.
5. The potential at O due to the large sphere (radius R, density $\rho$) is $V_1 = \frac{\rho}{3\epsilon_0} (\frac{3R^2}{2} - \frac{0^2}{2}) = \frac{\rho R^2}{2\epsilon_0}$.
6. The potential at O due to the negative sphere (radius $R' = R/2$, density $-\rho$) is $V_2$. Point O is at a distance $r = R/2$ from the center of this negative sphere (A). $V_2 = \frac{-\rho}{3\epsilon_0} (\frac{3R'^2}{2} - \frac{r^2}{2}) = \frac{-\rho}{3\epsilon_0} (\frac{3(R/2)^2}{2} - \frac{(R/2)^2}{2}) = \frac{-\rho}{3\epsilon_0} (\frac{3R^2}{8} - \frac{R^2}{8}) = -\frac{\rho R^2}{12\epsilon_0}$.
7. The total potential at O is $V_O = V_1 + V_2 = \frac{\rho R^2}{2\epsilon_0} - \frac{\rho R^2}{12\epsilon_0} = \frac{6\rho R^2 - \rho R^2}{12\epsilon_0} = \frac{5\rho R^2}{12\epsilon_0}$.