Question

A series LR circuit is connected to a voltage source with $V(t) = V_0 \sin \omega t$. After very large time, current $I(t)$ behaves as $(t_0 >> \frac{L}{R})$:

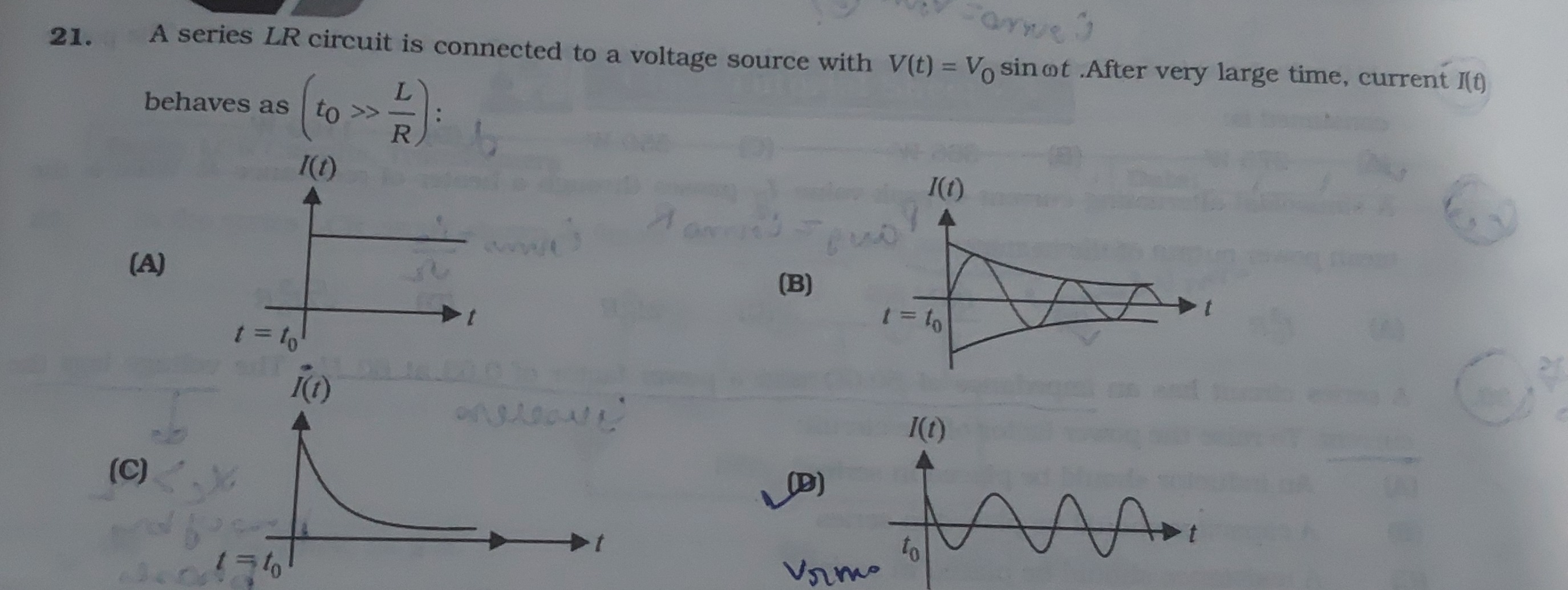
• A. constant current
• B. damped sinusoidal oscillation
• C. exponentially decaying current
• D. pure sinusoidal oscillation with a constant amplitude

Answer 1

Answer: (D)

D

Answer 2

When a series LR circuit is connected to an AC voltage source $V(t) = V_0 \sin \omega t$, the circuit undergoes both a transient response and a steady-state response.

1. Transient Response: This part of the current decays exponentially with time, characterized by the time constant $\tau = L/R$. The problem states "After very large time" $(t_0 >> L/R)$, which means the transient component has completely died out.
2. Steady-State Response: In the steady state, the current in the circuit will be a sinusoidal function with the same angular frequency $\omega$ as the applied voltage. The impedance of the LR circuit is $Z = \sqrt{R^2 + (\omega L)^2}$. The amplitude of the steady-state current is $I_0 = \frac{V_0}{Z} = \frac{V_0}{\sqrt{R^2 + (\omega L)^2}}$. The current will lag the voltage by a phase angle $\phi$, where $\tan \phi = \frac{\omega L}{R}$. Thus, the steady-state current can be expressed as $I(t) = I_0 \sin(\omega t - \phi)$.

This means that after a very large time, the current will be a purely sinusoidal wave with a constant amplitude $I_0$ and the same frequency as the source.

• (A) Shows a constant current. This is incorrect for an AC voltage source.
• (B) Shows a damped sinusoidal oscillation. This represents the transient part of the current, which dies out over time. The question asks for the behavior after a very large time, meaning the transient has already died out.
• (C) Shows an exponentially decaying current. This is characteristic of a DC circuit's transient response, not a steady-state AC response.
• (D) Shows a pure sinusoidal oscillation with a constant amplitude. This accurately represents the steady-state current in an LR circuit connected to an AC voltage source.

Therefore, option (D) correctly depicts the current behavior after a very large time.