Question
Question: (a + 2) sin $\alpha$ + (2a - 1) cos $\alpha$ = (2a + 1) if tan $\alpha$ = ...
(a + 2) sin α + (2a - 1) cos α = (2a + 1) if tan α =
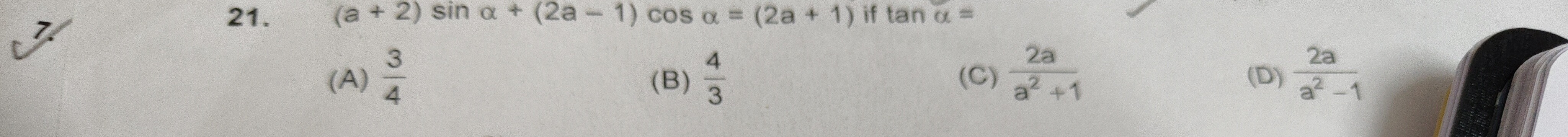
43
34
a2+12a
a2−12a
34
Solution
The given equation is (a+2)sinα+(2a−1)cosα=(2a+1).
We can solve this equation by using the tangent half-angle substitution: Let t=tan(α/2). Then sinα=1+t22t and cosα=1+t21−t2.
Substitute these into the given equation: (a+2)(1+t22t)+(2a−1)(1+t21−t2)=(2a+1)
Multiply both sides by (1+t2) to clear the denominators: 2t(a+2)+(2a−1)(1−t2)=(2a+1)(1+t2)
Expand the terms: 2at+4t+2a−2at2−1+t2=2a+2at2+1+t2
Rearrange the terms to form a quadratic equation in t: Collect t2 terms: −2at2+t2−2at2−t2=−4at2 Collect t terms: 2at+4t=(2a+4)t Collect constant terms: 2a−1−2a−1=−2
So the equation becomes: −4at2+(2a+4)t−2=0 Divide by -2: 2at2−(a+2)t+1=0
This is a quadratic equation in t. We can solve for t using the quadratic formula t=2a−b±b2−4ac: t=2(2a)−(−(a+2))±(−(a+2))2−4(2a)(1) t=4aa+2±(a+2)2−8a t=4aa+2±a2+4a+4−8a t=4aa+2±a2−4a+4 t=4aa+2±(a−2)2 t=4aa+2±∣a−2∣
This gives two possible values for t:
- t1=4aa+2+(a−2) (assuming a−2≥0, i.e., a≥2) t1=4a2a=21
- t2=4aa+2−(a−2) (assuming a−2≥0, i.e., a≥2) t2=4a4=a1
If a−2<0, i.e., a<2, then ∣a−2∣=−(a−2)=2−a.
- t1=4aa+2+(2−a)=4a4=a1
- t2=4aa+2−(2−a)=4aa+2−2+a=4a2a=21
So, the two possible values for t=tan(α/2) are 21 and a1.
Now we find tanα using the formula tanα=1−t22t:
Case 1: If t=21 tanα=1−(1/2)22(1/2)=1−1/41=3/41=34
Case 2: If t=a1 tanα=1−(1/a)22(1/a)=1−1/a22/a=a2a2−12/a=a2⋅a2−1a2=a2−12a
We have two potential solutions for tanα: 34 and a2−12a. Let's check which of these solutions are valid by substituting them back into the original equation.
For tanα=34: If tanα=34, then we can have sinα=54,cosα=53 (for α in Q1) or sinα=−54,cosα=−53 (for α in Q3).
Substitute sinα=54 and cosα=53 into the original equation: (a+2)(54)+(2a−1)(53)=2a+1 54a+8+56a−3=2a+1 510a+5=2a+1 2a+1=2a+1 This is true for all values of a. Thus, tanα=34 is always a valid solution.
For tanα=a2−12a: This value is option (D). The value 34 is option (B). Since this is a single choice question, and both solutions are mathematically derived and valid, there might be a specific condition on a that makes them equivalent, or one is preferred. If the two solutions are equal: 34=a2−12a 4(a2−1)=6a 4a2−4=6a 4a2−6a−4=0 2a2−3a−2=0 Factoring the quadratic: (2a+1)(a−2)=0 This implies a=2 or a=−21. If a=2, then tanα=22−12(2)=34. So both solutions are identical. If a=−1/2, then tanα=(−1/2)2−12(−1/2)=1/4−1−1=−3/4−1=34. So both solutions are identical.
Since the question asks for "if tan α =", it implies a unique value or a value that is always true. As tanα=34 is always a solution regardless of a (as long as a is such that the original expression is defined, which it is for any real a), it is the most general answer. The option a2−12a depends on a. In multiple choice questions, if a constant solution is derived that holds true for all values of the parameter, it is usually the intended answer unless specified otherwise.
