Question

The statement $[(p \rightarrow q) \land \sim q] \rightarrow r$ is a tautology, when is equivalent to [2023]

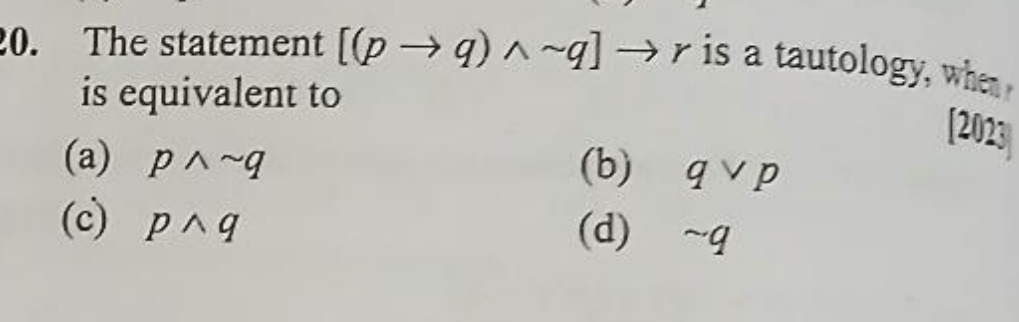
• A. $p \land \sim q$
• B. $q \lor p$
• C. $p \land q$
• D. $\sim q$

Answer 1

Answer: (D)

$\sim q$

Answer 2

1. Rewrite the given implication:

   $$[(p\to q) \land \sim q] \to r \quad \text{is equivalent to} \quad (\sim p \lor q) \land \sim q \to r.$$

2. Simplify the antecedent:

   $$(\sim p \lor q) \land \sim q = (\sim p \land \sim q) \lor (q \land \sim q).$$

   Since $q \land \sim q$ is always false,

   $$(\sim p \lor q) \land \sim q = \sim p \land \sim q.$$

3. The implication becomes:

   $$(\sim p\land \sim q) \to r \quad \text{which is equivalent to} \quad \sim (\sim p \land \sim q) \lor r.$$

   Using De Morgan's law:

   $$\sim (\sim p \land \sim q) = p \lor q.$$

   Thus, the statement is:

   $$(p \lor q) \lor r.$$

4. For the entire statement to be a tautology, the only "critical" case is when the antecedent $\sim p \land \sim q$ is true (i.e. when $p = F$ and $q = F$). In that case, $r$ must be true. Notice though that for $q = F$, whether $p$ is true or false, $r$ is forced only when both $p$ and $q$ are false. This condition is captured exactly by the option:

   $$\sim q.$$

   Thus, choosing $r = \sim q$ will ensure that whenever $q$ is false (and hence when the antecedent might be true), $r$ will be true, making the implication a tautology.

Explanation (Minimal):

• $p \to q$ is equivalent to $\sim p \lor q$.
• $(\sim p \lor q) \land \sim q$ simplifies to $\sim p \land \sim q$.
• $(\sim p \land \sim q) \to r$ must be true in the case $p=F$ and $q=F$, so $r$ must be true when $q$ is false.
• Hence, $r$ must be equivalent to $\sim q$.