Question
Question: The number of (+) ve integral solution of $\frac{x^2(3x-4)^3(x-2)^4}{(x-5)^5(2x-7)^6}\leq0$ is...
The number of (+) ve integral solution of
(x−5)5(2x−7)6x2(3x−4)3(x−2)4≤0 is
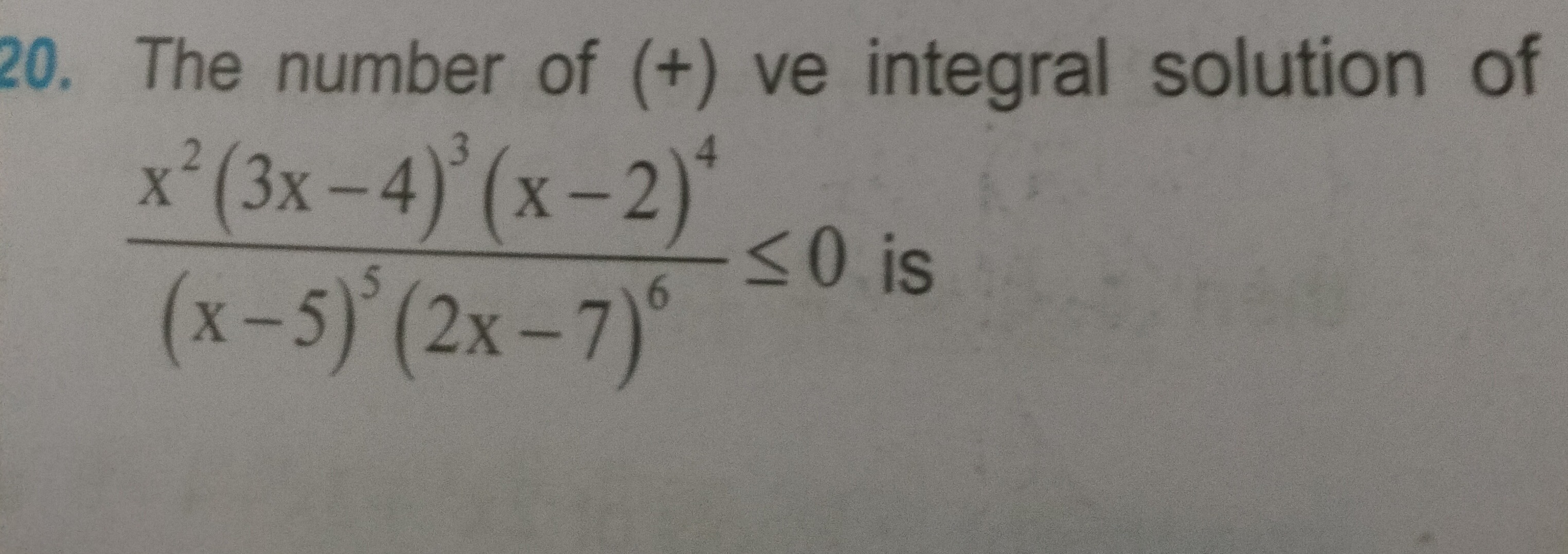
3
Solution
To solve the inequality (x−5)5(2x−7)6x2(3x−4)3(x−2)4≤0, we follow these steps:
-
Identify Critical Points: Set each factor in the numerator and denominator to zero to find the critical points:
- x2=0⟹x=0 (Even power, so no sign change across x=0)
- (3x−4)3=0⟹3x−4=0⟹x=4/3 (Odd power, so sign changes across x=4/3)
- (x−2)4=0⟹x−2=0⟹x=2 (Even power, so no sign change across x=2)
- (x−5)5=0⟹x−5=0⟹x=5 (Odd power, so sign changes across x=5)
- (2x−7)6=0⟹2x−7=0⟹x=7/2 (Even power, so no sign change across x=7/2)
Order the critical points on a number line: 0,4/3(≈1.33),2,7/2(=3.5),5.
-
Analyze Signs in Intervals (Wavy Curve Method): Pick a test value in the rightmost interval, say x=6: (6−5)5(2⋅6−7)662(3⋅6−4)3(6−2)4=(1)5(5)636(14)3(4)4=positivepositive>0. So, for x>5, the expression is positive.
Now, move left across the critical points, changing the sign only when crossing a critical point with an odd power:
- For x>5: Positive (+)
- At x=5 (odd power): Sign changes. So, x∈(7/2,5) is Negative (-).
- At x=7/2 (even power): Sign does not change. So, x∈(2,7/2) is Negative (-).
- At x=2 (even power): Sign does not change. So, x∈(4/3,2) is Negative (-).
- At x=4/3 (odd power): Sign changes. So, x∈(0,4/3) is Positive (+).
- At x=0 (even power): Sign does not change. So, x∈(−∞,0) is Positive (+).
Summary of signs:
- x∈(−∞,0): Positive
- x∈(0,4/3): Positive
- x∈(4/3,2): Negative
- x∈(2,7/2): Negative
- x∈(7/2,5): Negative
- x∈(5,∞): Positive
-
Determine the Solution Set for ≤0: We need the intervals where the expression is negative (<0) or zero (=0).
- Where expression is negative: x∈(4/3,2)∪(2,7/2)∪(7/2,5). This can be compactly written as x∈(4/3,5) excluding x=2 and x=7/2.
- Where expression is zero: The numerator becomes zero. This occurs at x=0, x=4/3, and x=2.
- Excluded points: The denominator cannot be zero. So, x=5 and x=7/2.
Combining these, the solution set for (x−5)5(2x−7)6x2(3x−4)3(x−2)4≤0 is: x∈{0}∪[4/3,7/2)∪(7/2,5).
-
Find Positive Integral Solutions: We are looking for positive integers (x>0 and x is an integer) that satisfy the inequality.
- x=0 is not a positive integer.
- Consider the interval [4/3,7/2)∪(7/2,5).
- 4/3≈1.33
- 7/2=3.5
- 5
- Integers in [1.33,3.5):
- x=2: 2∈[1.33,3.5), and it makes the expression zero, so it's a solution.
- x=3: 3∈[1.33,3.5), and it makes the expression negative, so it's a solution.
- Integers in (3.5,5):
- x=4: 4∈(3.5,5), and it makes the expression negative, so it's a solution.
The positive integral solutions are 2,3,4. The number of positive integral solutions is 3.
The final answer is 3.
Explanation of the solution:
- Identify critical points from numerator and denominator: 0,4/3,2,7/2,5.
- Use the wavy curve method. Factors with even powers (x2, (x−2)4, (2x−7)6) do not change the sign across their critical points. Factors with odd powers ((3x−4)3, (x−5)5) change the sign.
- Test an interval (e.g., x>5) to determine the initial sign. For x>5, the expression is positive.
- Move left across critical points, applying sign changes based on power parity.
- (5,∞): +
- (7/2,5): - (sign change at 5 due to odd power)
- (2,7/2): - (no sign change at 7/2 due to even power)
- (4/3,2): - (no sign change at 2 due to even power)
- (0,4/3): + (sign change at 4/3 due to odd power)
- (−∞,0): + (no sign change at 0 due to even power)
- Identify regions where the expression is ≤0. This includes intervals where it's negative and points where it's zero.
- Negative intervals: (4/3,2)∪(2,7/2)∪(7/2,5).
- Zero points (from numerator): x=0,x=4/3,x=2.
- Excluded points (from denominator): x=5,x=7/2.
- Combine: The solution set is {0}∪[4/3,7/2)∪(7/2,5).
- Find positive integers in this set: x=2,3,4.
- Count the solutions: There are 3 positive integral solutions.
