Question
Question: Let $y = y(t)$ be a solution to the differential equation $y' + 2ty = t^2$, then $16 \lim_{t\to\inft...
Let y=y(t) be a solution to the differential equation y′+2ty=t2, then 16limt→∞ty is:
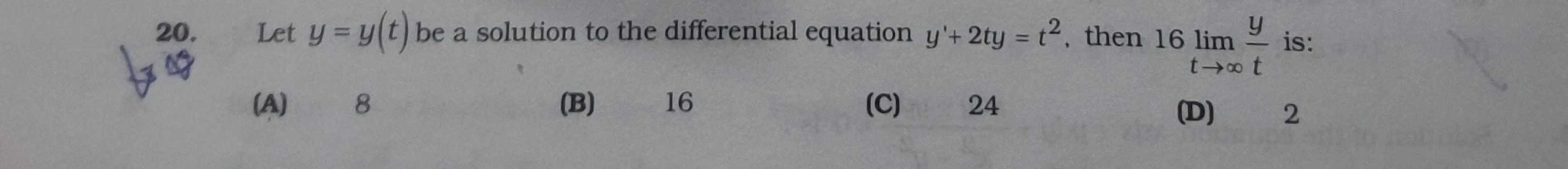
8
16
24
2
8
Solution
The given differential equation is a first-order linear differential equation of the form y′+P(t)y=Q(t), where P(t)=2t and Q(t)=t2.
Step 1: Find the integrating factor (IF). The integrating factor is given by IF=e∫P(t)dt. IF=e∫2tdt=et2.
Step 2: Write the general solution. The general solution for a linear differential equation is y⋅IF=∫Q(t)⋅IFdt+C. Substituting the values: yet2=∫t2et2dt+C So, y(t)=e−t2∫t2et2dt+Ce−t2.
Step 3: Evaluate the limit limt→∞ty. We need to find limt→∞te−t2∫t2et2dt+Ce−t2. We can split this into two parts: limt→∞te−t2∫t2et2dt+limt→∞tCe−t2
The second term: limt→∞tCe−t2=0, because e−t2 approaches 0 much faster than t approaches infinity.
For the first term, rewrite it as limt→∞tet2∫t2et2dt. This limit is of the indeterminate form ∞∞, so we can apply L'Hopital's Rule.
Let F(t)=∫t2et2dt. By the Fundamental Theorem of Calculus, F′(t)=t2et2. Let G(t)=tet2. G′(t)=dtd(tet2)=1⋅et2+t⋅(et2⋅2t) (using product rule and chain rule) G′(t)=et2+2t2et2=et2(1+2t2).
Applying L'Hopital's Rule: limt→∞G′(t)F′(t)=limt→∞et2(1+2t2)t2et2 =limt→∞1+2t2t2
To evaluate this limit, divide the numerator and the denominator by the highest power of t in the denominator, which is t2: =limt→∞t21+t22t2t2t2 =limt→∞t21+21 As t→∞, t21→0. So, the limit is 0+21=21.
Therefore, limt→∞ty=21.
Step 4: Calculate the final expression. We need to find 16limt→∞ty. 16×21=8.
The final answer is 8.
Explanation of the solution (minimal) The differential equation y′+2ty=t2 is a first-order linear DE. The integrating factor is IF=e∫2tdt=et2. Multiplying by IF, we get dtd(yet2)=t2et2. Integrating both sides gives yet2=∫t2et2dt+C. So, y(t)=e−t2∫t2et2dt+Ce−t2. We need to find limt→∞ty=limt→∞te−t2∫t2et2dt+Ce−t2. The term limt→∞tCe−t2=0. For the main term, limt→∞tet2∫t2et2dt, apply L'Hopital's Rule. Derivative of numerator is t2et2. Derivative of denominator is et2(1+2t2). The limit becomes limt→∞et2(1+2t2)t2et2=limt→∞1+2t2t2=limt→∞1/t2+21=21. Thus, limt→∞ty=21. Finally, 16limt→∞ty=16×21=8.
