Solveeit Logo
Login

Question

Question: 20. \(\displaystyle \int \tan^{-1} (\sec x + \tan x)\,dx =\)...

  1. ∫tan⁡−1(sec⁡x+tan⁡x) dx=\displaystyle \int \tan^{-1} (\sec x + \tan x)\,dx =
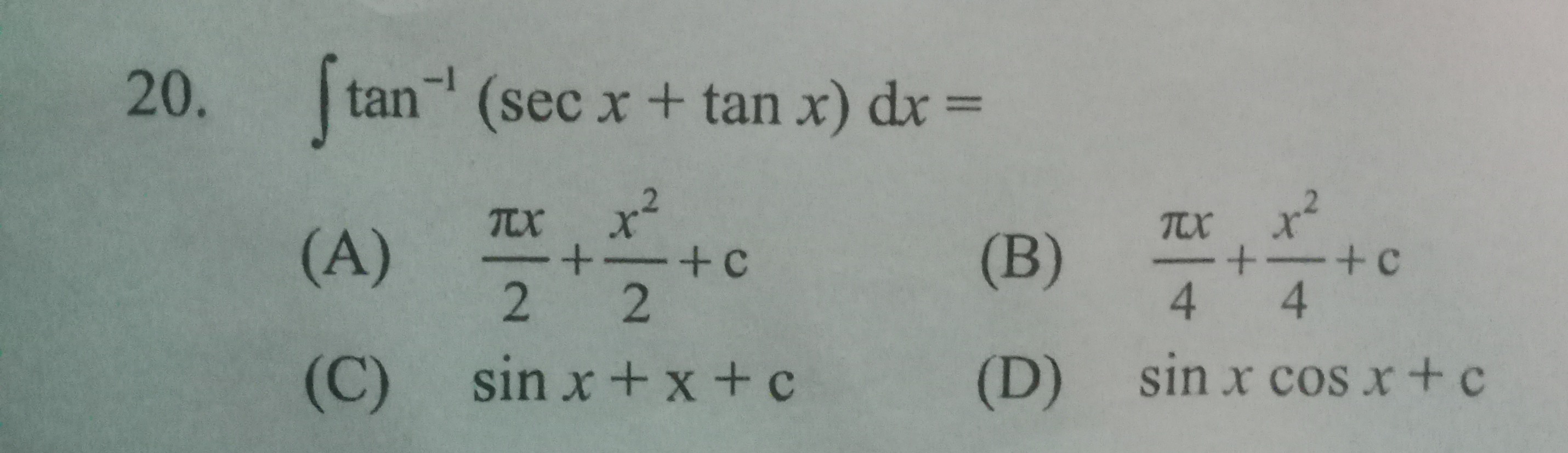
A

πx2+x22+c\displaystyle \frac{\pi x}{2} + \frac{x^2}{2} + c

B

πx4+x24+c\displaystyle \frac{\pi x}{4} + \frac{x^2}{4} + c

C

sin⁡x+x+c\displaystyle \sin x + x + c

D

sin⁡xcos⁡x+c\displaystyle \sin x\cos x + c

Answer

πx4+x24+c\displaystyle \frac{\pi x}{4} + \frac{x^2}{4} + c

Explanation

Solution

Key idea:

  1. Use the half‑angle identity:
sec⁡x+tan⁡x=1+tan⁡2 ⁣x2+2tan⁡x21−tan⁡2 ⁣x2=( 1+tan⁡x2 )2(1−tan⁡x2)(1+tan⁡x2)=1+tan⁡x21−tan⁡x2=tan⁡ ⁣(π4+x2).\sec x + \tan x = \frac{1+\tan^2\!\tfrac x2 + 2\tan\tfrac x2}{1-\tan^2\!\tfrac x2} = \frac{(\,1+\tan\tfrac x2\,)^2}{(1-\tan\tfrac x2)(1+\tan\tfrac x2)} = \frac{1+\tan\tfrac x2}{1-\tan\tfrac x2} = \tan\!\Bigl(\tfrac\pi4 + \tfrac x2\Bigr).
  1. Therefore
tan⁡−1(sec⁡x+tan⁡x)=π4+x2.\tan^{-1}(\sec x + \tan x) = \tfrac\pi4 + \tfrac x2.
  1. Integrate term‑wise:
∫ ⁣(π4+x2) dx=π4 x+12 x22+C=πx4+x24+C.\int\!\Bigl(\tfrac\pi4 + \tfrac x2\Bigr)\,dx = \tfrac\pi4\,x + \tfrac1{2}\,\frac{x^2}{2} + C = \frac{\pi x}{4} + \frac{x^2}{4} + C.