Question
Question: If the lines $\frac{2x-4}{\lambda}=\frac{y-1}{2}=\frac{z-3}{1}$ and $\frac{x-1}{1}=\frac{3y-1}{\lamb...
If the lines λ2x−4=2y−1=1z−3 and 1x−1=λ3y−1=1z−2 are perpendicular to other, then λ=
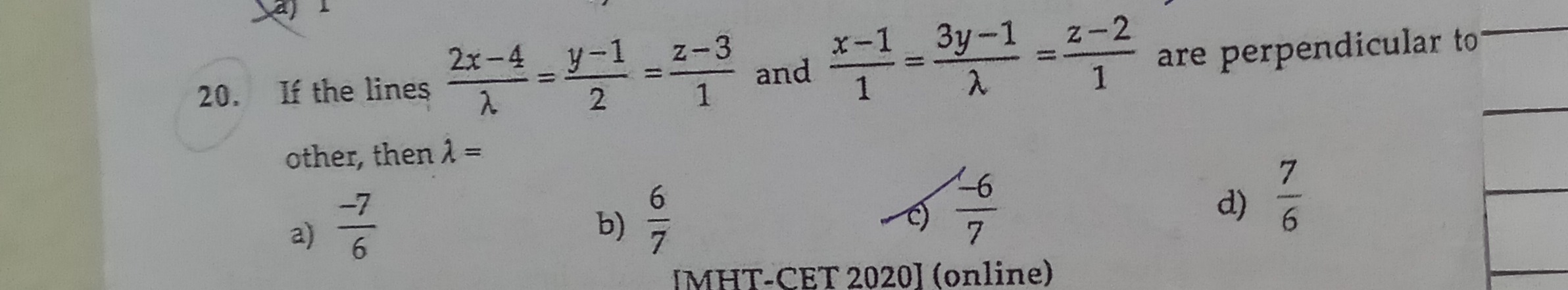
6−7
76
7−6
67
7−6
Solution
To find the value of λ, we first need to express the given lines in standard form and determine their direction vectors.
The first line is given as: λ2x−4=2y−1=1z−3
We can rewrite this as: λ2(x−2)=2y−1=1z−3
Which simplifies to: λ/2x−2=2y−1=1z−3
Thus, the direction vector for the first line, d1, is (2λ,2,1).
The second line is given as: 1x−1=λ3y−1=1z−2
We can rewrite this as: 1x−1=λ3(y−31)=1z−2
Which simplifies to: 1x−1=λ/3y−31=1z−2
Thus, the direction vector for the second line, d2, is (1,3λ,1).
Since the lines are perpendicular, their direction vectors are orthogonal, meaning their dot product is zero: d1⋅d2=0
So, we have: (2λ)(1)+(2)(3λ)+(1)(1)=0
This simplifies to: 2λ+32λ+1=0
Multiplying the entire equation by 6 to eliminate fractions: 3λ+4λ+6=0
Combining terms: 7λ+6=0
Solving for λ: 7λ=−6 λ=7−6
Therefore, the value of λ is 7−6.
