Question

If $\alpha$ and $\beta$ are the roots of the equation, $a\cos\theta + b\sin\theta = c$ then match the entries of column-I with the entries of column-II.

Column-I

(A) $\sin\alpha + \sin\beta$ (B) $\sin\alpha.\sin\beta$ (C) $\tan \frac{\alpha}{2} + \tan \frac{\beta}{2}$ (D) $\tan \frac{\alpha}{2} . \tan \frac{\beta}{2} =$

Column-II

(P) $\frac{2b}{a+c}$ (Q) $\frac{c-a}{c+a}$ (R) $\frac{2bc}{a^2+b^2}$ (S) $\frac{c^2-a^2}{a^2+b^2}$

Answer 1

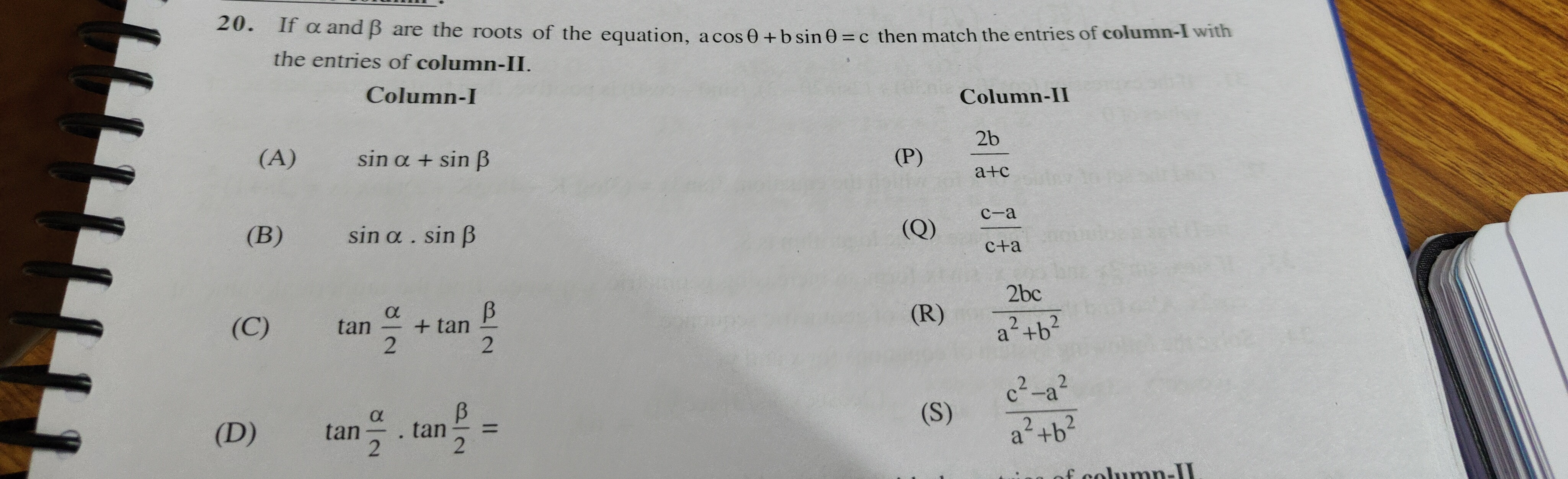
A-R, B-S, C-P, D-Q

Answer 2

To solve the problem, we need to transform the given trigonometric equation into quadratic equations in terms of $\sin\theta$ and $\tan(\theta/2)$ respectively.

The given equation is $a\cos\theta + b\sin\theta = c$.

Part 1: Finding $\sin\alpha + \sin\beta$ and $\sin\alpha \sin\beta$

To get a quadratic equation in $\sin\theta$, we isolate $\cos\theta$ and square both sides: $a\cos\theta = c - b\sin\theta$ Squaring both sides: $a^2\cos^2\theta = (c - b\sin\theta)^2$ Substitute $\cos^2\theta = 1 - \sin^2\theta$: $a^2(1 - \sin^2\theta) = c^2 - 2bc\sin\theta + b^2\sin^2\theta$ $a^2 - a^2\sin^2\theta = c^2 - 2bc\sin\theta + b^2\sin^2\theta$ Rearrange into a quadratic equation in $\sin\theta$: $(a^2+b^2)\sin^2\theta - 2bc\sin\theta + (c^2-a^2) = 0$

Let $\alpha$ and $\beta$ be the roots of the original equation. Then $\sin\alpha$ and $\sin\beta$ are the roots of this quadratic equation. Using Vieta's formulas: (A) Sum of roots: $\sin\alpha + \sin\beta = \frac{-(-2bc)}{a^2+b^2} = \frac{2bc}{a^2+b^2}$. This matches with (R) in Column-II. So, (A) $\to$ (R).

(B) Product of roots: $\sin\alpha \sin\beta = \frac{c^2-a^2}{a^2+b^2}$. This matches with (S) in Column-II. So, (B) $\to$ (S).

Part 2: Finding $\tan \frac{\alpha}{2} + \tan \frac{\beta}{2}$ and $\tan \frac{\alpha}{2} . \tan \frac{\beta}{2}$

To get a quadratic equation in $\tan(\theta/2)$, we use the half-angle tangent substitutions: $\cos\theta = \frac{1-\tan^2(\theta/2)}{1+\tan^2(\theta/2)}$ and $\sin\theta = \frac{2\tan(\theta/2)}{1+\tan^2(\theta/2)}$. Let $t = \tan(\theta/2)$. Substitute these into the original equation: $a\left(\frac{1-t^2}{1+t^2}\right) + b\left(\frac{2t}{1+t^2}\right) = c$ Multiply by $(1+t^2)$ to clear the denominators: $a(1-t^2) + 2bt = c(1+t^2)$ $a - at^2 + 2bt = c + ct^2$ Rearrange into a quadratic equation in $t$: $(c+a)t^2 - 2bt + (c-a) = 0$

Let $\alpha$ and $\beta$ be the roots of the original equation. Then $\tan(\alpha/2)$ and $\tan(\beta/2)$ are the roots of this quadratic equation. Using Vieta's formulas: (C) Sum of roots: $\tan \frac{\alpha}{2} + \tan \frac{\beta}{2} = \frac{-(-2b)}{c+a} = \frac{2b}{c+a}$. This matches with (P) in Column-II. So, (C) $\to$ (P).

(D) Product of roots: $\tan \frac{\alpha}{2} . \tan \frac{\beta}{2} = \frac{c-a}{c+a}$. This matches with (Q) in Column-II. So, (D) $\to$ (Q).

Summary of Matches: (A) $\to$ (R) (B) $\to$ (S) (C) $\to$ (P) (D) $\to$ (Q)