Question

If a mod 3 = 1 and b mod 3 = 2, where a, b $\in$ N, then choose the set of correct options.

(a mod b = c, a, b, c $\in$ N ; means a = nb + c where n $\in$ N)

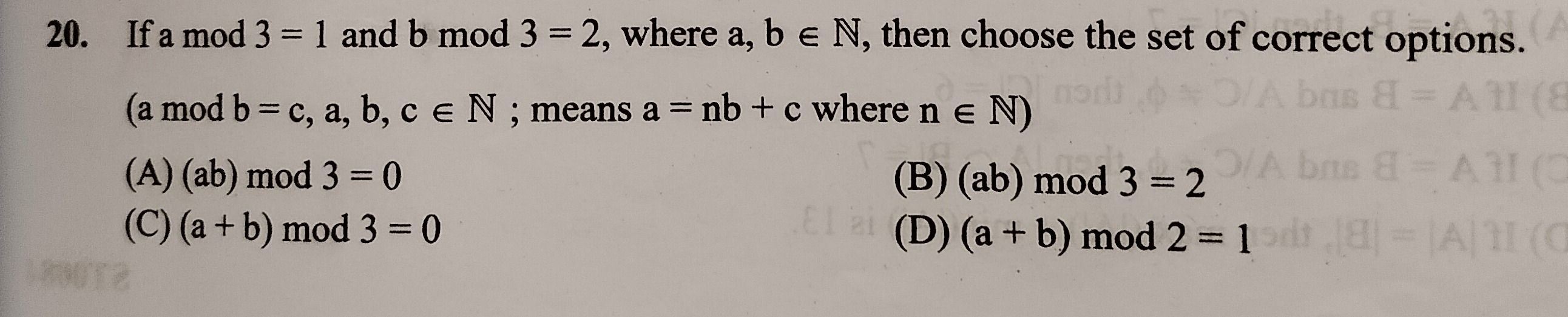
• A. (ab) mod 3 = 0
• B. (ab) mod 3 = 2
• C. (a + b) mod 3 = 0
• D. (a + b) mod 2 = 1

Answer 1

Answer: (B), (C)

Options B and C are correct.

Answer 2

Given:

$$a \equiv 1 \pmod{3} \quad \Rightarrow \quad a = 3k + 1$$ $$b \equiv 2 \pmod{3} \quad \Rightarrow \quad b = 3j + 2 \quad \text{(with } k,j \in \mathbb{N}\text{)}$$

Option A: $(ab) \mod 3 = 0$

Calculate:

$$ab = (3k+1)(3j+2) = 9kj + 6k + 3j + 2$$

Taking $\mod 3$, the terms $9kj$, $6k$, and $3j$ vanish (divisible by 3):

$$ab \equiv 2 \pmod{3}$$

Thus, Option A is false.

Option B: $(ab) \mod 3 = 2$

From above, we clearly have $ab \equiv 2 \pmod{3}$.

Thus, Option B is correct.

Option C: $(a+b) \mod 3 = 0$

Calculate:

$$a+b = (3k+1) + (3j+2) = 3k + 3j + 3 = 3(k+j+1)$$

Clearly, $a+b$ is a multiple of 3.

Thus, Option C is correct.

Option D: $(a+b) \mod 2 = 1$

Since:

$$a+b = 3(k+j+1)$$

the parity depends on $k+j+1$, which can be even or odd. For example:

• If $k = 0$ and $j = 0$, then $a+b = 3$ (odd, so $\equiv 1 \pmod{2}$).
• If $k = 0$ and $j = 1$, then $a+b = 6$ (even, so $\equiv 0 \pmod{2}$).

Thus, the statement is not always true. Option D is false.