Question

If $A = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 1 & -3 \\ -1 & 2 & 3 \end{bmatrix}$, then $A_{31} + A_{32} + A_{33} =$

where $A_{ij}$ is cofactor of $a_{ij}$, where $A = [a_{ij}]_{3x3}$

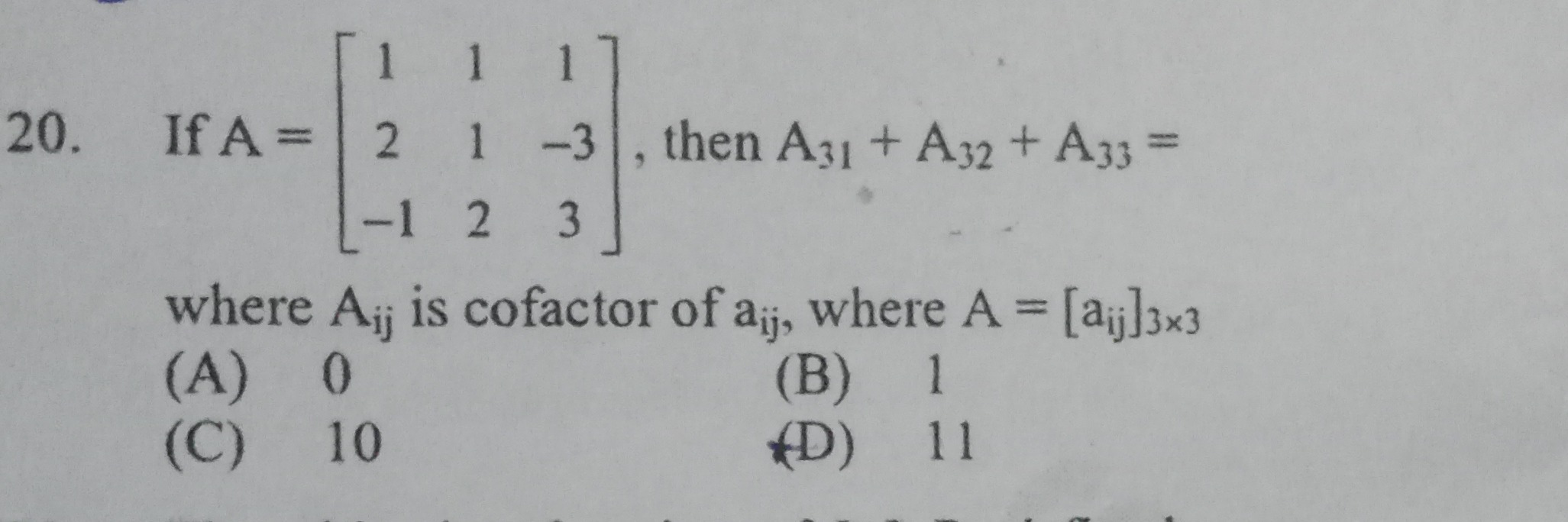
• A. 0
• B. 1
• C. 10
• D. 11

Answer 1

Answer: (A)

0

Answer 2

To find $A_{31} + A_{32} + A_{33}$, we need to calculate the cofactors $A_{31}$, $A_{32}$, and $A_{33}$ of the matrix $A$.

1. Calculate $A_{31}$: $A_{31} = (-1)^{3+1} M_{31} = M_{31}$. $M_{31}$ is the determinant of the submatrix obtained by deleting the 3rd row and 1st column of $A$: $M_{31} = \det \begin{bmatrix} 1 & 1 \\ 1 & -3 \end{bmatrix} = (1)(-3) - (1)(1) = -3 - 1 = -4$. So, $A_{31} = -4$.

2. Calculate $A_{32}$: $A_{32} = (-1)^{3+2} M_{32} = -M_{32}$. $M_{32}$ is the determinant of the submatrix obtained by deleting the 3rd row and 2nd column of $A$: $M_{32} = \det \begin{bmatrix} 1 & 1 \\ 2 & -3 \end{bmatrix} = (1)(-3) - (1)(2) = -3 - 2 = -5$. So, $A_{32} = -(-5) = 5$.

3. Calculate $A_{33}$: $A_{33} = (-1)^{3+3} M_{33} = M_{33}$. $M_{33}$ is the determinant of the submatrix obtained by deleting the 3rd row and 3rd column of $A$: $M_{33} = \det \begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} = (1)(1) - (1)(2) = 1 - 2 = -1$. So, $A_{33} = -1$.

Now, find the sum $A_{31} + A_{32} + A_{33}$: $A_{31} + A_{32} + A_{33} = -4 + 5 + (-1) = 1 - 1 = 0$.

Therefore, $A_{31} + A_{32} + A_{33} = 0$.